As superfícies e do tubo indicado na figura possuem áreas e , respectivamente. Um líquido de densidade escoa pelo tubo e apresenta, no ponto , velocidade e pressão . Determine a velocidade e a pressão do líquido no ponto .
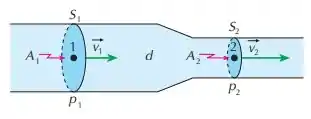
Passo 1
Shoow galerinhaa !!
Acabamos de ver que trabalhar com a equação de Bernoulli pode parecer cabuloso mas no fundo é bem tranquilo e bem legal!
A primeira coisa que o problema nos pediu foi a velocidade na seção , certo?
De cara a Equação de Bernoulli não nos ajuda porque ela precisa dessas duas coisas que estão sendo pedidas
Mas nós temos a Equação da Continuidade, não é? Então vamos usá-la
Isolando a velocidade no ponto , vamos passar a área para o outro lado dividindo
O problema nos disse que:
Substituindo:
Tomem cuidado com as unidades, nesse caso não precisamos converter porque tem em cima e em baixo e eles acabam se anulando. A unidade de será o que restou
Passo 2
Agora precisamos achar a pressão no ponto , certo?
E agora sim é a vez dela, a Equação de Bernoulli!!
Pelo desenho vemos que a altura do ponto central de cada seção é igual:
Substituindo:
Como o termo está presente nos dois lados com o mesmo sinal (), eles se cancelam:
Sabendo que:
Só nos resta substituir, não é?
Precisamos resolver essa conta. Primeiro faremos as divisões
Agora elevaremos os números que estão ao quadrado
Podemos multiplicar os parênteses
Agora precisamo tomar um pouco de cuidado. Perceba que as potências de não estão com o mesmo expoente, precisamos fazer com que esses expoentes fiquem iguais.
Para isso, transformaremos o
E nossa equação fica
O termo passa para o outro lado da igualdade com sinal contrário:
Nesse momento vai fazer sentido ter transformado as potências de para o mesmo expoente, agora podemos colocar o em evidência!
Shooow!!