Pretende-se medir a velocidade de um líquido que escoa por uma canalização. Para isso, insere-se na canalização um tubo de Venturi, conforme a figura (: desnível do líquido existente nos tubos verticais; : aceleração da gravidade; e : áreas das seções transversais e ).
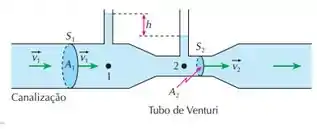
Prove que:
Passo 1
Faaaala meus queridos, vamos seguir?!
Essa questão é daquelas que só envolve letras. Vamos ver como fica.
Queremos a velocidade, não é?! Então vamos usar a Equação de Bernoulli:
A altura do ponto central das duas seções é a mesma, então:
Na fórmula:
Como o termo está nos dois lados da igualdade com o mesmo sinal podemos cancelar:
Não temos quase nada! Eita lasqueira!!
Mas vamos fazer uma manipulação matemática e mandar a pressão de para o outro lado da igualdade com sinal contrário, assim como o termo
Essa variação de pressão nós temos uma fórmula para ela, não é?
Caso não lembram, eu mostro pra vocês:
Então:
Como a densidade está presente em todos os termos, vamos cortar:
Multiplicando todos os termos por para facilitar a nossa vida lá na frente:
Passo 2
Com isso nós conseguimos calcular a velocidade ?
Que nada, não é? Porque não temos a velocidade em !!
E aqui trazemos novamente a equação da continuidade, lembrando que a vazão nos dois pontos são iguais:
Isolando a velocidade no ponto , vamos passar a área para o outro lado dividindo:
Substituindo na equação do Passo :
Colocando o em evidência
Vamos passar o termo que acompanha a velocidade para o outro lado dividindo:
Tiramos a raíz dos dois lados:
E chegamos ao fim de mais umaa!! Bem legal, não é?!