Para melhorar a dissipação térmica em um chip de silício, quadrado com , um pino de cobre é fundido à superfície do chip. O comprimento e o diâmetro do pino são e , respectivamente, e ar atmosférico a e está em escoamento cruzado em relação ao pino.
A superfície do chip, e portanto a base do pino, é mantida a uma temperatura de .
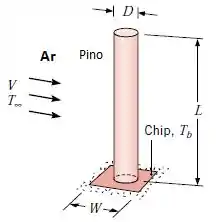
Supondo que o chip cause um efeito desprezível sobre o escoamento ao redor do pino, qual é o coeficiente convectivo médio na superfície do pino?
Desprezando a radiação e supondo que o coeficiente convectivo na extremidade do pino seja igual ao calculado na parta , determine a taxa de transferência de calor no pino.
Desprezando a radiação e supondo que o coeficiente de transferência de calor na superfície exposta do chip seja igual ao calculado na parte , determine a taxa total de transferência de calor saindo do chip.
Passo 1
Supondo que o chip cause um efeito desprezível sobre o escoamento ao redor do pino, qual é o coeficiente convectivo médio na superfície do pino?
Antes de qualquer coisa, precisamos saber as propriedades dos materiais que vamos precisar para resolver o problema.
Começando pelo ar e utilizando como referência a temperatura de filme, dada por:
A essa temperatura, de acordo com a tabela A.4:
Já para o cobre que está à temperatura de , de acordo com a tabela A.1, temos que:
Show! Agora já podemos seguir em frente!
Passo 2
O próximo passo é calcular o número de Reynolds, dado por:
Agora podemos partir para o número de Nusselt.
Passo 3
De acordo com a correlação de Hilpert, o número de Nusselt médio é dado por:
Para o valor do número de Reynolds que encontramos, temos que:
Logo:
Passo 4
O coeficiente convectivo médio será dado por:
Substituindo os valores:
![]()
Passo 5
Desprezando a radiação e supondo que o coeficiente convectivo na extremidade do pino seja igual ao calculado na parta , determine a taxa de transferência de calor no pino.
Para aletas com convecção na extremidade, a taxa de transferência de calor é dada por:
Onde:
Substituindo os valores:
Substituindo os valores de e na expressão de , teremos:
![]()
Ufa!
Passo 6
Desprezando a radiação e supondo que o coeficiente de transferência de calor na superfície exposta do chip seja igual ao calculado na parte , determine a taxa total de transferência de calor saindo do chip.
A taxa de transferência total de calor saindo do chip será dada por:
Onde representa a taxa de calor retirado do chip por convecção, dessa forma:
Onde:
Substituindo os valores:
Resposta
![]()
![]()
![]()