Suponha que você tenha uma escolha entre duas aletas pino. Uma possui uma área de seção reta quadrada com de lado e de altura e outra possui uma área de seção reta circular com de diâmetro e de altura.
Ambas são construídas de alumínio puro (propriedades à ). Em torno de cada aleta existe um ar circulando em velocidade de e temperatura de temperatura do meio é .
Assuma que o ar possui propriedades constantes e iguais a seu valor a 300 K. A base da aleta está a . Qual dessas terá a melhor relação (mais favorável em termos térmicos) de taxa de transferência de calor por peso de material para compor a aleta?
Despreze eventuais efeitos de convecção natural.
Passo 1
Antes de qualquer coisa, vamos pegar as propriedades do alumínio e do ar a . De acordo com a tabela A.4, para o ar:
Para o alumínio puro, de acordo com a tabela A.1:
Passo 2
A taxa de transferência de calor pode ser calculada da seguinte forma:
Assim, a primeira coisa que faremos será determinar o coeficiente convectivo para cada caso.
Passo 3
Para encontrar o coeficiente convectivo, precisamos do número de Reynolds, dado por:
Assim, para o pino circular:
Para o pino retangular:
Passo 4
O número de Nusselt será dado por
Para o pino circular, de acordo com o valor do número de Reynolds que encontramos, temos que:
Logo:
Para o pino retangular, como o valor que encontramos para o número de Reynolds está fora do intervalo tabelado, vamos usar a seguinte equação:
Passo 5
O coeficiente convectivo será:
Passo 6
Precisamos calcular agora o desempenho das aletas, para isso, vamos usar soluções tabeladas, onde, para a aleta circular:
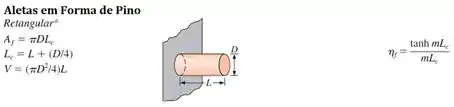
Logo:
Para a aleta retangular:
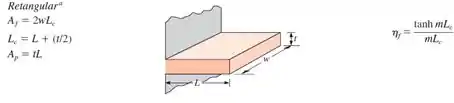
Logo:
Passo 7
A taxa de transferência de calor para a aleta circular será:
Para a aleta retangular:
Passo 8
O peso da aleta circular será:
O peso da aleta retangular será:
Passo 9
A relação entre taxa de transferência de calor por peso de material para cada aleta será:
Aleta circular:
Aleta retangular:
Assim, a aleta retangular possui a melhor relação de taxa de transferência de calor por peso de material para compor a aleta.
Resposta
A aleta retangular possui a melhor relação de taxa de transferência de calor por peso de material para compor a aleta.