Apresente a extensão par da função
e esboce o gráfico no intervalo .
Passo 1
Antes de começar o exercício propriamente dito, é primordial aqui você começar com a seguinte reflexão, meu caro filósofo:
“O que é uma função par?”
Poxa, funções pares, lá da teoria, é uma função que tem uma reflexão no eixo . A função é uma função par, pois olha o gráfico dela:
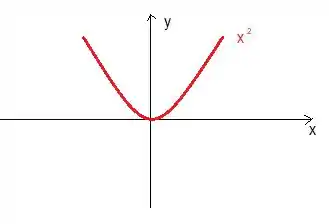
O que vamos ter que fazer, basicamente é colocar a nossa função com esse tipo de reflexão (ao redor do eixo ). Assim ela se torna par!
Outra boa pergunta então a se fazer agora é: quem é a nossa função ?
Passo 2
A melhor forma de saber quem é uma função, é desenhando, então vamos lá!
Essa é a nossa função. Pra desenhar, basta você colocar as curvas de cada intervalo no gráfico. Por sorte, as nossas curvas são retas:
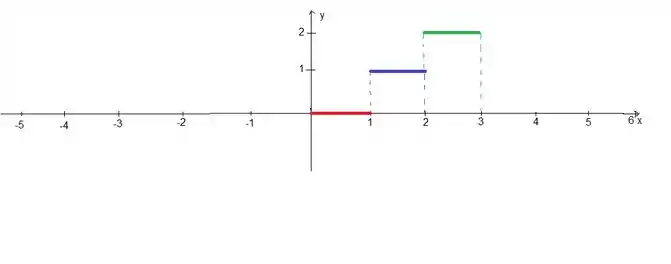
Passo 3
Então, agora é só você pegar a reflexão dessa função do outro lado do gráfico para transforma-la em par:
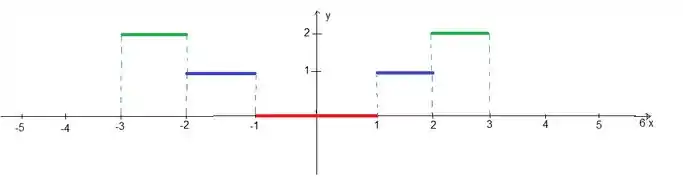
E claro, agora colocar esse padrão se repetir em todo o (como se pegasse ele e puxasse), pois a extensão em si deve ser periódica:
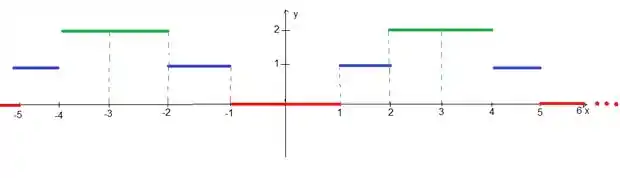
Prontinho! Graficamente temos a nossa extensão par. Mas e matematicamente? Como representamos isso?
Passo 4
Aqui a gente tem que pegar a extensão gráfica...
E anotá-la matematicamente falando.
Pow, perceba que a função de a é :
De até e de a a função é :
E de e , bem como de a a função é igual a :
Como vimos, a função é periódica de extensão par e de período , então podemos falar que...