Dada a função:
(b) Esboço o gráfico da série de Fourier de obtida no item (a) no intervalo [-6,6]
Passo 1
Pelo teorema da convergência da série de Fourier, temos que:
O gráfico da série de Fourier no intervalo [-6,6] está desenhado na figura abaixo, destacando o valor da série de Fourier nos ponto de descontinuidade de f.
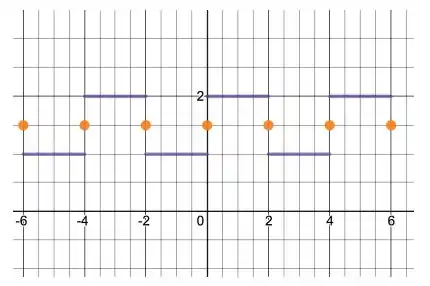
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Em cada um dos problemas de 15 a 22:(a) Encontre a série de Fourier indicada para a função dada.(b) Esboce o gráfico da função para a qual a série converge em um intervalo de três períodos.15. f x = 1
Determine se a função dada é par, ímpar, ou nenhuma das duas. x 3
36. A partir da série de Fourier para a onda triangular (Exemplo 1 da Seção 10.2), mostre que π 8 2 = 1 + 1 3 2 + 1 5 2 + … = ∑ n = 0 ∞ 1 2 n + 1 2
35. A partir da série de Fourier da onda quadrada no Exemplo 1 da Seção 10.3, mostre que π 4 = 1 - 1 3 + 1 5 - 1 7 + … = ∑ n = 0 ∞ - 1 n 2 n + 1 Essa relação entre π e os inteiros positivos ímpares fo
37. Suponha que f tem uma série de Fourier em senos f x = ∑ n = 1 ∞ b n sen n π x L 0 ≤ x ≤ L (a) Mostre, formalmente, que 2 L ∫ 0 L f x 2 d x = ∑ n = 1 ∞ b n 2 Compare esse resultado (equação de Pa