Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fluido sendo acelerado

Ver Teoria
Exercício 81234567

Enunciado

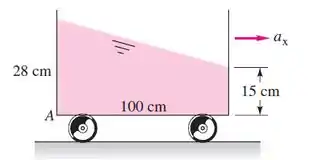
(Adaptada) O tanque de líquido da Figura acelera para a direita com o fluido em movimento de corpo rígido. (a) Calcule a x   em m/s². (b) Determine a pressão manométrica no ponto A se o fluido for glicerina a 20°C.

Passo 1

Para calcular a aceleração em x, vamos analisar a geometria do problema.

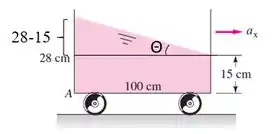
O fluido está inclinado a um certo ângulo θ. A tangente desse ângulo é o cateto oposto (28-15cm) sobre o adjacente (100 cm). Então:

tan ⁡ θ =   28 - 15 100 =   13 100 = 0,13

Pela teoria de fluido acelerando, vimos outra fórmula para tangente de θ :

tan ⁡ θ =   a x g + a y

No nosso exercício, não há componente y da aceleração, logo a y = 0 .

tan ⁡ θ =   a x g

Substituindo:

0,13 =   a x 9,8

Logo:

a x = 1,28 m s 2

Encontramos a componente x da aceleração conforme pede a letra a.

Passo 2

Para encontrar a pressão manométrica no ponto A, podemos usar essa fórmula:

P 1 - P 2 = ρ . a x . x + ρ . g - a y . y

Sendo P A ,   m a n =   P A ,   a b s - P a t m =   P 1 - P 2

Lembrando que:

a x = 1,28   m / s ² a y = 0 m s 2

Como o fluido é glicerina, ρ = 1260   k g / m ³

Além disso, x = 100   c m = 1     m e y = 15   c m =   0,15   m

Substituindo:

P A ,   m a n = 1260 × 1,28 × 1 + 1260 × 9,8 - 0 × 0,15

Então:

P A ,   m a n = 3460   P a

E assim encontramos a pressão manométrica em A! 😊

Resposta

  1. a x = 1,28 m s 2
  2. P A ,   m a n = 3460   P a

Exercícios de Livros Relacionados

3.129AanálisedoProblema3.121sugerequetalvezsejapossíveldeterminarocoeficientedeatritodedeslizamentoentreduas superfíciespelamedidadoângulodasuperfícielivreemumrecipientecontendolíquidoedeslizandoparab
Se o tubo em U do Problema 3.117 for centrifugado a 300 rpm, qual será a pressão em A? Se uma pequena trinca aparecer em A , quanta água será perdida em D ?
Um micromanômetro centrífugo pode ser usado para criar pequenas e precisas pressões diferenciais no ar para trabalhos de medição de alta precisão. O dispositivo consiste em um par de discos paralelos
Um tubo de ensaio é girado em uma centrifuga. O suporte do tubo é montado em um pivô de modo que o tubo báscula para fora à medida que a rotação aumenta. Para altas velocidades, o tubo fica aproximada
Um balde cilíndrico, com diâmetro e altura de 400m m , pesa 15 N e contém água até uma altura de 200 mm. O balde é girado a 5m / s em uma trajetória circular vertical de raio igual a 1 m. Suponha que