Uma caixa retangular, contendo fluido de densidade , é colocada em um carrinho que desce uma ladeira com aceleração constante . A inclinação da ladeira é de . Determine a inclinação da superfície livre, usando o sistema de coordenadas indicado na figura.
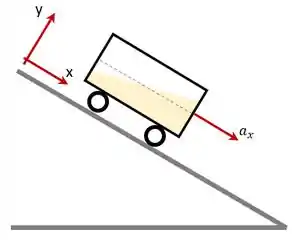
Passo 1
Bom, se vamos usar o sistema de coordenadas da figura, então vamos ter que decompor a aceleração da gravidade nessas duas direções.
Para decompor temos que encontrar o ângulo que a força peso está fazendo com uma delas:
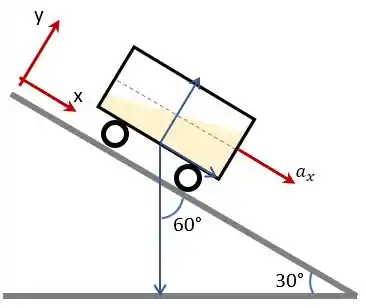
Como a aceleração da gravidade faz com a horizontal e o plano está inclinado , então a aceleração da gravidade tem um ângulo de com a aceleração .
Assim, decompondo a aceleração da gravidade temos:
Beleza, agora, podemos calcular o ângulo de inclinação do fluido:
Tá ligado que a gente viu que:
Mas repara que ali na figura o líquido nem tá indo pra trás como ele deveria devido à aceleração. Isso acontece porque o peso tá puxando ele pra trás. Então, aqui a gente vai usar:
Vamos adotar como positivo o sentido para baixo e para direita. Assim, temos: