Um tanque selado, cheio com fluido de densidade , é acelerado a para a direita. Determine as pressões nos pontos e da figura, sabendo-se que a pressão no manômetro é . As dimensões do tanque estão na figura.
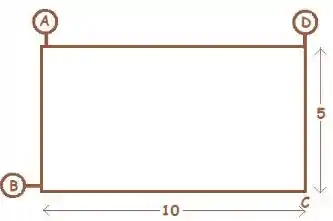
Passo 1
Como o tanque é selado o fluido não consegue se movimentar, assim a diferença de pressão será dada por:
Beleza, como foi dado a pressão no ponto , vamos calcular a pressão em relação aquele ponto. A densidade do líquido também foi dada , assim como a aceleração, que é toda em x, . E a gravidade a gente vai considerar .
Então vamos começar calculando a pressão no ponto . Observando a posição desse ponto em relação ao ponto , a gente vê que e
E no ponto , que está a e