Uma caixa, cuja base horizontal tem e altura , está com líquido pela metade (veja a figura). Determine a aceleração horizontal, constante, , que resulta na condição crítica do enchimento, definido como sendo aquela para a qual há a ameaça do derramamento. Determine também a equação que indica a variação da pressão ao longo da base na condição crítica. A caixa está aberta à atmosfera.
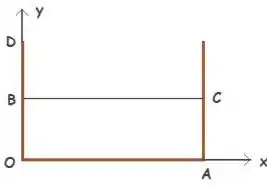
Passo 1
O primeiro passo é descobrir para qual ângulo de inclinação o fluido estará no limite de escapar da caixa.
Para a água escapar ela tem que subir na extremidade esquerda, se ela sobe isso de um lado do outro ela desce, assumindo assim a seguinte condição:
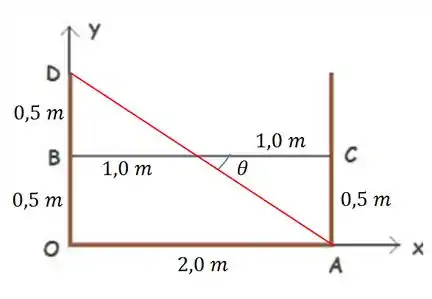
O valor desse ângulo é fácil descobrirmos:
Agora podemos usar aquela formula que vimos na teoria:
No nosso caso, e é o que queremos descobrir, assim:
Passo 2
Agora, vamos montar a equação de variação de pressão na base
Vimos na teoria que a fórmula para calcular variação de pressão entre dois pontos é:
será a posição , já que a posição inicial estará em . A questão é que quando você anda para o lado a profundidade do ponto aumenta linearmente.
Qual é a equação de
é dado por uma função de primeiro grau, pois aumenta linearmente, certo? Então pode ser escrita assim:
Se quando então .
Agora falta só descobrir .
Beleza, então a função de é:
Assim, podemos montar a equação de pressão assim
Onde é a pressão atmosférica.