Considere a figura abaixo. Se a aceleração linear na direção for igual a e a aceleração linear na direção for , encontre a equação das isobáricas e a pressão nos pontos , , e . O fluido é óleo, de densidade .
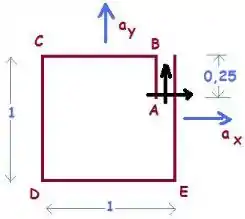
Passo 1
Vamos começar esclarecendo que quando ele pede para determinar a equação da isobárica, ele está pedido que determinasse o ângulo de inclinação do fluido. Pois assim, saberemos que naquela direção a pressão é a mesma.
Beleza, então vamos começar calculando isso. Vimos que a fórmula para calcular essa inclinação é:
Assumindo a direção positiva para baixo, assim temos:
Passo 2
Agora, vamos calcular as pressões em cada ponto. O ponto é o ponto de referencia, nele sabemos que a pressão é a pressão atmosférica.
Para a gente calcular a diferença de pressão entre dois pontos, temos que saber a distância em e entre esses dois pontos.
O ponto , está na posição e . Já o ponto está na e .
Jogando da equação de pressão, temos:
Substituindo o e da posição , temos:
Vamos fazer o mesmo para o ponto , que está na posição e .
Lembra que adotamos que o sentido positivo é para baixo, e assim o sentido positivo de é para esquerda. Vamos calcular a pressão em .
O ponto , agora. Ele está na posição e .
E por fim o ponto que está na posição e