O tanque abaixo está movendo com aceleração constante subindo um plano inclinado de , como mostra a Figura abaixo. Considerando o movimento de corpo rígido, calcule o valor da aceleração , se a aceleração é para cima ou para baixo e a pressão manométrica no ponto se o fluido for mercúrio a .
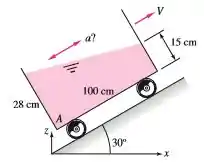
Passo 1
O primeiro passo que precisamos fazer é descobrir o ângulo que o liquido está fazendo com o plano do tanque. Para isso vamos usar as alturas e comprimentos que o enunciado deu:
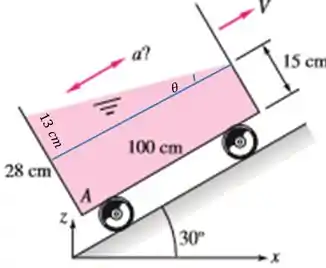
Só que a formula que vimos é para calcular o ângulo com a horizontal. Então vamos descobrir quanto vale ele. Descobrimos que esse ângulo vale com um plano que foi inclinado da horizontal, então basta voltar os . Sendo assim, o ângulo que queremos é:
Beleza, agora podemos aplicar a formula que vimos para o ângulo de inclinação de um fluido
Precisamos decompor em componentes e .
A aceleração é na mesma direção do plano inclinado, assim ela faz com o eixo . Lembra do macete “Co-lado/Se-parado”. Pois vamos decompor , assim, como sabems que ele faz com .
E
Como adotamos o sentido positivo para baixo para esquerda, então e
Beleza, agora podemos calcular o valor da aceleração:
Conseguimos dizer o quanto da aceleração está em cada direção:
E
Sendo que como deu positivo, significa que a aceleração é para baixo.
Passo 2
Agora, vamos calcular a pressão no ponto e para isso vamos usar aquela fórmula boladona que aprendemos:
Temos quase tudo para calcular a pressão no ponto . Falta apenas descobrirmos a distância normal entre a superfície de mercúrio e o ponto .
Bem, usando um pouco de trigonometria, vamos chegar lá.
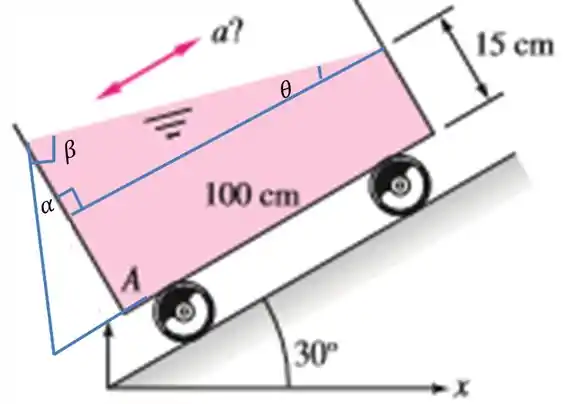
Chegamos que
Assim,
Assim, podemos dizer que
Agora, substituindo os dados que temos na equação de pressão, lembrando que a densidade do mercúrio é .