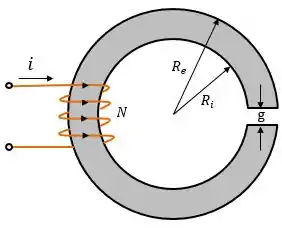
O circuito magnético abaixo consiste em anéis de material magnético dispostos em uma pilha de altura . Os anéis têm raio interno e externo . Suponha que o ferro tenha permeabilidade infinita , e despreze os efeitos de dispersão e de espraiamento magnéticos. Para:
Calcule:
O comprimento médio do núcleo e a área da seção reta
A relutância do núcleo e a do entreferro .
Para espiras, calcule:
a indutância .
A corrente requerida para que se opere com uma densidade de fluxo no entreferro de .
O fluxo concatenado correspondente a da bobina.
Passo 1
O comprimento médio do núcleo será o comprimento da circunferência de raio
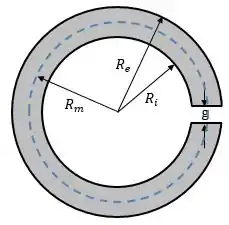
Subtraído do comprimento do entreferro, ou seja:
Passo 2
A área da seção reta pode ser calculada dando um corte na pilha, tendo a seção reta abaixo:
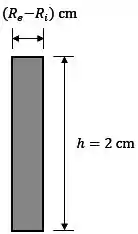
Então,
Passo 3
Vamos começar calculando a relutância do núcleo. A fórmula é:
Como foi dito no enunciado que , então a relutância do núcleo é zero.
Passo 4
A relutância do entreferro tem a seguinte fórmula:
Lembrando que :
Então, a relutância total desse circuito magnético:
Passo 5
A equação que relaciona a relutância com a indutância é:
Como o enrolamento tem espiras, temos:
Passo 6
Para uma densidade de fluxo de no entreferro, o fluxo no núcleo será:
Logo, a gerada será:
Passo 7
Como
A corrente pode ser calculada assim:
Passo 8
O fluxo concatenado da bobina pode ser calculado pela fórmula abaixo: