Um indutor deve ser projetado usando um núcleo magnético com a forma dada pela figura abaixo:
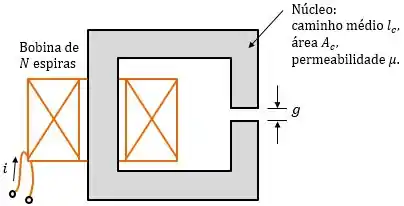
O núcleo tem seção reta uniforme de área e comprimento médio . Calcule o comprimento do entreferro e o número de espiras tais que a indutância seja e de modo que o indutor possa operar com corrente de pico de sem saturação. Suponha que a saturação ocorra quando a densidade de fluxo de pico do núcleo exceda a e que, abaixo da saturação, o núcleo tenha permeabilidade .
Passo 1
Vamos começar calculando a relutância do núcleo. A fórmula é:
Como foi dito no enunciado que abaixo da saturação , então a relutância do núcleo será:
Passo 2
A relutância do entreferro tem a seguinte fórmula:
Lembrando que :
Passo 3
Então, a relutância total desse circuito magnético:
Passo 4
A equação que relaciona a relutância com a indutância é:
Como o queremos uma indutância de :
Passo 5
Como a densidade de fluxo máxima é e a área é , podemos calcular o fluxo que circula por esse núcleo.
Passo 6
Podemos calcular a pela fórmula abaixo:
Como , temos:
Como a corrente é :
Passo 7
Temos duas equações com duas incógnitas:
Então, vamos isolar na primeira equação e substituí-lo na segunda:
Como o número de espiras não pode ser zero, temos:
Passo 8
Agora que temos o número de espiras, vamos substituir em uma das equações para encontrarmos o comprimento do entreferro. Da primeira equação, temos:
Como :