Um circuito magnético com um único entreferro está mostrado na figura abaixo. As dimensões do núcleo são:
Área da seção reta
Comprimento médio do núcleo
Comprimento do entreferro
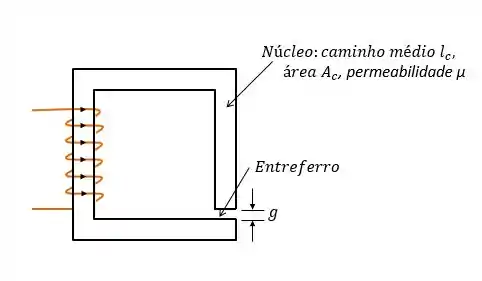
Supondo uma permeabilidade de núcleo infinita , calcule:
O número necessário de espiras para obter uma indutância de .
A corrente no indutor que resultará em uma densidade de fluxo de .
Passo 1
Vamos começar calculando a relutância do núcleo. A fórmula é:
Como foi dito no enunciado que , então a relutância do núcleo é zero:
Passo 2
A relutância do entreferro tem a seguinte fórmula:
Lembrando que :
Passo 3
A equação que relaciona o número de espiras com a indutância é:
A relutância total é a própria relutância do entreferro, já que a relutância do núcleo é zero. Então, para uma indutância de , temos:
Passo 4
Para uma densidade de fluxo de , o fluxo no núcleo será:
Logo, a gerada será:
Passo 5
Como
A corrente pode ser calculada assim: