O indutor abaixo tem as seguintes dimensões:
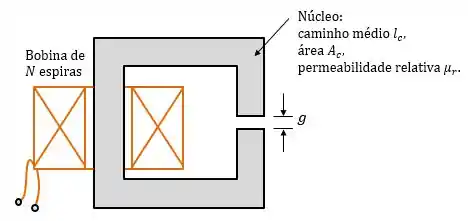
Desprezando os campos de espraiamento no entreferro e de dispersão e supondo , calcule a indutância.
Passo 1
Vamos começar calculando a relutância do núcleo. A fórmula é:
Como foi dito no enunciado que , então a relutância do núcleo será:
Passo 2
A relutância do entreferro tem a seguinte fórmula:
Lembrando que :
Passo 3
Então, a relutância total desse circuito magnético:
Passo 4
A equação que relaciona a relutância com a indutância é:
Como o enrolamento tem espiras, temos: