Um copo é lavado com água a e é colocado de boca para baixo em uma mesa. O ar ambiente a que foi aprisionado no copo é aquecido até . No processo de aquecimento, ocorrem vazamentos, de modo que, quando a temperatura do ar no copo atinge o valor fornecido, a pressão do ar no copo é acima da pressão ambiente de . Após algum tempo, a temperatura do ar aprisionado no copo volta a ser igual à do ambiente. Determine a pressão no interior do copo, sabendo que a pressão atmosférica é .

O enunciado diz que um copo aprisiona ar dentro dele. Como o copo está mais quente que o ar, o ar é aquecido até atingir uma temperatura de . Quando ele chega nessa temperatura, sua pressão vale acima da pressão atmosférica de . Ou seja, sua pressão vale .

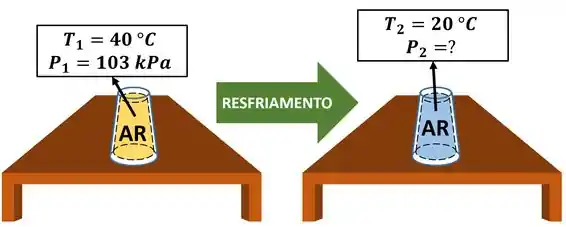
Vamos chamar esse estado, definido por essas duas propriedades, é o estado 1.

Depois, o ar é resfriado junto com o copo, sem vazar, até chegar na temperatura do ambiente . O enunciado pede para calcularmos o valor da pressão depois que o ar é resfriado. Chamamos o estado do ar resfriado de estado 2.

Durante o resfriamento, nosso sistema composto pelo ar continua ocupando o mesmo volume e continua com a mesma quantidade de mol do início do processo de resfriamento. Em outras palavras, o processo ocorre com o valor de volume constante e com o número de mole constante.

Se a gente reorganizar a fórmula de gás ideal, podemos perceber melhor uma dica que vai nos ajudar muito.

O lado direito da segunda equação acima tem valor constante durante todo processo de resfriamento, porque as três variáveis presentes nele são constantes. Como a pressão dividida pela temperatura é igual ao lado direito, seu valor também é constante durante todo o processo.

Por causa disso, descobrimos que:

Se a gente passar a temperatura para o outro lado multiplicando, encontramos a fórmula para calcular .

Pronto, agora que temos a fórmula podemos partir para o cálculo. Essa parte vai ficar no próximo passo de resolução do exercício!