Gás hélio armazenado em um tanque de aço de a e é utilizado para encher um balão. Quando a pressão cai para , o fluxo de hélio é interrompido. Se todo o hélio ainda estiver a , qual terá sido o tamanho do balão produzido?
Passo 1
O exercício é pra achar o volume do balão, depois de um tanque cheio de hélio terminar de enchê-lo. Para organizar a solução desse problema, chamaremos de estado 1 o estado em que o tanque está fechado e ainda não encheu o balão.
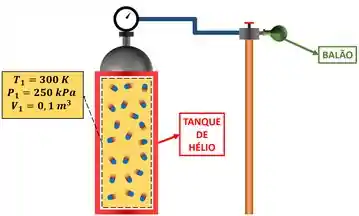
Nesse estado 1, o enunciado diz que a pressão , a temperatura e o volume do hélio valem:
O balão é enchido de hélio até a pressão do tanque cair para . Isso significa que a pressão no tanque e a pressão no balão se equilibraram. Por isso o hélio do tanque não tem mais força para entrar no balão. O enunciado também diz que o hélio não varia de temperatura durante o processo de enchimento.
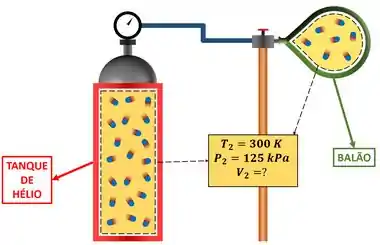
Chamamos de estado 2 o estado do hélio depois do enchimento. Nesse momento, o hélio está tanto no tanque quanto no balão. Ou seja, nesse caso, o nosso sistema o nosso sistema é tanto o hélio presente no tanque, quanto o hélio presente no balão. As propriedades do estado 2 informadas na questão foram:
Vamos deixar para o próximo passo as informações do enunciado que estão mais escondidas e precisam de uma interpretação de texto mais cuidadosa!
Passo 2
Como nosso sistema é todo o hélio, ele não varia sua quantidade de moles ao longo do processo de enchimento. Ele muda de lugar, mas sua massa total continua a mesma. Logo:
Podemos achar com a fórmula de gás ideal para o estado 1.
O enunciado quer saber o volume do balão depois do enchimento. Esse volume é igual ao volume do sistema no estado 2 ( é o volume do balão mais volume do tanque) menos o volume do sistema no estado 1 ( é o volume do tanque).
Já sabemos quanto vale , mas quanto vale ? Descobrimos isso, aplicando a fórmula de gás ideal ao estado 2.
Já foi mostrado como calcular todos os valores da equação acima! Então vamos começar nossos cálculos no próximo passo!
Passo 3
Vamos tentar achar primeiro o número de moles de hélio que forma nosso sistema:
Sabemos que o número de moles do sistema não varia do estado 1 para o estado 2.
Agora só falta descobrir o valor do volume no estado 2 para calcular o volume do balão.
O volume do balão é: