Inicialmente, um tanque rígido, com volume de , contém a e . Suponha que ocorra o vazamento acidental de de para a atmosfera. Sabendo que a temperatura final do no tanque, após o vazamento é , determine a pressão final. Considere a massa molar de igual a .
Passo 1
O sistema termodinâmico desse problema é o nitrogênio presente em um tanque rígido. Antes de ocorrer um vazamento de (estado 1) a pressão no tanque valia e a temperatura do gás valia .
Além disso, o volume ocupado pelo nitrogênio no estado 1 era:
Depois de vazar de (estado 2) o gás ficou com uma temperatura de . A pressão de nesse estado final é a incógnita do problema.
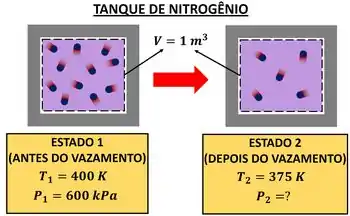
Pode parecer que esses foram os principais dados fornecidos pelo enunciado, mas existe uma informação muito importante escondida nele: como o tanque é rígido, mesmo após o vazamento, seu espaço não mudou. Ou seja, no estado 1 e no estado 2 o gás nitrogênio ocupa o mesmo volume.
Para encontrar a pressão final utilizaremos a equação do gás perfeito reorgazinada.
Só que ainda não sabemos como calcular e .
A fórmula de é:
A massa molar do gás nitrogênio vale:
A massa final do gás está em função da massa antes do vazamento . Logo precisamos saber calcular primeiro. O seu valor é encontrado com a equação de gás perfeito modificada.
Depois de fazer todos esses cálculos teremos condições de descobrir a pressão final no tanque. Mas deixaremos essa etapa pro passo seguinte!
Passo 2
Precisamos começar com o cálculo de .
Com esse valor podemos calcular .
Agora estamos prontos para calcular .
Sabendo isso, chegamos ao cálculo final de .