G2 de Cálculo 1 - MAT1161 da PUCRIO - 2012.1

Calcule:

Calcule:

Um triângulo retângulo, localizado no primeiro quadrante, tem um vértice na origem e seus outros dois vértices determinados pela interseção da reta tangente ao gráfico da função com os eixos coordenados (ver figura).

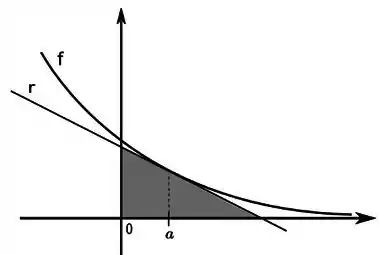
Determine a equação da reta tangente ao gráfico da em .

Determine as interseções da reta com o eixo e com o eixo .

Determine o valor de de forma que a área do triângulo seja máxima, considerando somente os triângulos formados no quadrante.

Considere

é contínua em ? é derivável em ?

Calcule e .

Determine os pontos críticos de .

Em quais intervalos é crescente?

Em quais intervalos é decrescente?

Determine, se houver, os pontos de mínimo local de .

Determine, se houver, os pontos de máximo local de .

Em quais intervalos, se houver, o gráfico de é côncavo para cima?

Em quais intervalos, se houver, o gráfico de é côncavo para baixo?

Determine, se houver, os pontos de inflexão do gráfico de .

Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .