O gráfico a seguir representa a derivada de uma função contínua em .
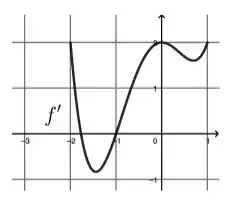
Sobre é INCORRETO afirmar que:
- é crescente em
- tem ponto de inflexão em
- ́e côncava para cima em
- tem um mínimo local em
- tem um máximo local em
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de cálculo 1. Uma bem clássica de análise de gráfico

Nosso objetivo é descobrir qual das alternativas está incorreta. Então vamos começar pela primeira.
Ela diz que é crescente em . E aí, é verdade? Bem, o que uma função precisa para ser crescente? Ela tem que ter derivada positiva, né? Então vamos olhar o gráfico da derivada nesse intervalo
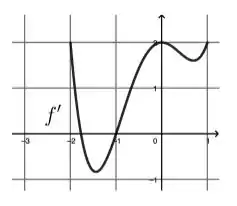
Ora, podemos observar que nesse intervalo a derivada é positiva, logo a função é crescente. Então já sabemos que a primeira afirmação é verdadeira. Vamos para a segunda
Passo 2
A segunda afirmação diz que tem ponto de inflexão em . E aí, tem mesmo? Vale lembrar que um ponto de inflexão é aquele onde temos uma mudança na concavidade da função, ou seja, é o ponto(s) onde a derivada segunda é igual a zero.
Mas nós só temos o gráfico da derivada primeira, como pegamos informação da derivada segunda?

Bem, vamos lembrar que a derivada segunda é a derivada da derivada primeira. Que nós temos. E sabemos que os pontos onde a derivada de uma função é zero são os pontos onde a função para de crescer e começa a decrescer e vice-versa. Ou seja, são os pontos de ótimo locais.
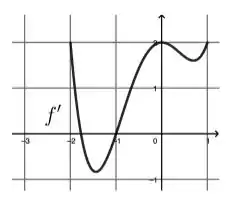
E ao olharmos o gráfico de vemos que é justamente um desses pontos. Logo a segunda afirmação é verdadeira.
Passo 3
A terceira afirmação diz que ́e côncava para cima em . E aí, será que é verdade? Vamos olhar o gráfico
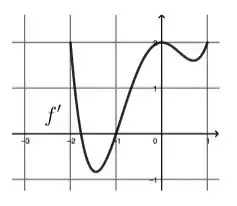
Bem, para ser côncava para cima, precisamos que a derivada segunda seja positiva. E como a derivada segunda é a derivada de . Ela ser positiva quer dizer que é crescente. E fica claro ao olharmos o gráfico que é crescente em . Então a terceira afirmação é verdadeira.
Vamos para a quarta afirmação. Ela diz que tem um mínimo local em . Bem em tem um ponto crítico, pois nesse ponto é zero. Mas é um mínimo? Ao analisarmos o gráfico, vemos que antes de , está decrescendo e depois de começa a crescer. O que implica que esse ponto é de mínimo local. Logo a quarta afirmação está correta,
Ou seja, só restou a última afirmação. Que necessariamente terá que ser falsa.

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊