Uma função tem as seguintes propriedades
-
i) é crescente em _____ e decrescente em ______ .
ii) ́ é côncava para cima em _____ e côncava para baixo em _____ .
iii)́ ______ é um ponto de máximo local e ___________ é um ponto de inflexão do gráfico de .
- Esboce o gráfico de
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de cálculo 1. Uma bem clássica de desenho de gráfico

Vamos começar pela letra nela, temos que preencher uma série de espaços vazios. Então vamos começar revisando as informações do enunciado e a primeira parte dessa questão
i) é crescente em _____ e decrescente em ______
Então, queremos saber quais regiões a função é crescente e em quais ela é decrescente. Mas o que será que indica crescimento de uma função? O sinal da primeira derivada!!!! Se ele for positivo, a função cresce, e se for negativo decresce. Então ao analisarmos as informações do enunciado temos:
Ou seja,
i) é crescente em __ e decrescente em __
Passo 2
Agora, vamos para o item 2 da letra a)
́ é côncava para cima em _____ e côncava para baixo em _____ .
então, queremos saber quais regiões a função é côncava para cima ou para baixo. Mas o que será que indica a concavidade de uma função? O sinal da segunda derivada!!!! Se ele for positivo, a função é côncava para cima, e se for negativo, côncava para baixo. Então ao analisarmos as informações do enunciado temos:
Ou seja, ́ é côncava para cima em __ e côncava para baixo em __ .
Para finalizarmos a letra a, temos o item 3
______ é um ponto de máximo local e ___________ é um ponto de inflexão do gráfico de .
Queremos os pontos de máximo e de inflexão do gráfico de . Bem, pontos de máximo é aquele onde a primeira derivada é zero, e além disso, a derivada a esquerda desse ponto é positiva e a direita negativa. Então olhando as informações do enunciado temos:
Como a função está bem definida para , então é um ponto onde a derivada é zero e é um ponto de máximo
Um ponto de inflexão é aquele onde a derivada segunda é zero. Então olhando as informações do enunciado temos:
Como a função está bem definida para , então é um ponto onde a derivada segunda é zero e é um ponto de inflexão
Logo
__ __ é um ponto de máximo local e ___ __ é um ponto de inflexão do gráfico de .
Passo 3
Por fim, desenhamos o gráfico de , usando as informações do enunciado
temos que: é uma assíntota vertical. concluímos isso da última informação
temos que : é a única assíntota horizontal de , concluímos isso da penúltima informação
Juntando isso com as informações de crescimento e concavidade que descobrimos nos outros passos podemos desenhar o gráfico.
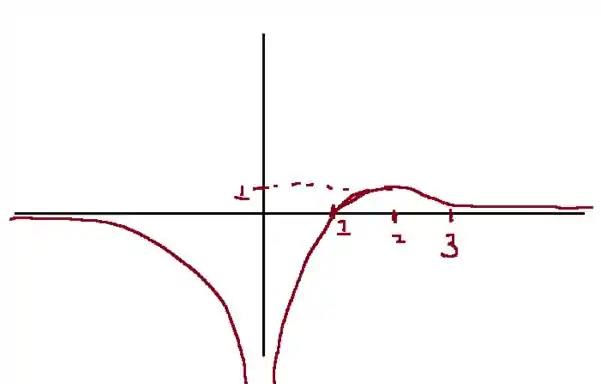

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊