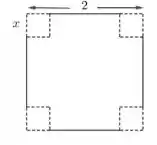
Uma caixa é feita retirando-se quatro quadrados dos cantos de uma folha de papel quadrada de lado e dobrando os lados, como na figura. O tamanho dos lados dos quadrados retirados para que o volume da caixa seja máximo pertence ao intervalo:
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de cálculo 1. Uma bem clássica de otimização.

Nosso objetivo é descobrir qual é o valor de , de forma que o volume da caixa obtida dobrando a figura abaixo seja o maior possível.
Passo 2
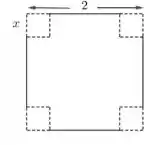
Qual seria a estratégia para resolver essa questão? Isso ae, deriva e iguala a zero. Mas o que vamos derivar? A equação que descreve o volume da caixa, certo? Então vamos construir essa equação.
O volume de uma caixa é definido pela área da base vezes a altura da caixa. Ao analisarmos a nossa figura,
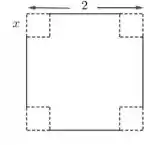
Podemos ver que a altura da caixa é (que é a parte que cortamos para poder dobrar), mas e qual é a área da base? Bem será , já que os lados da base tem tamanho . Então o volume é:
Derivando temos:
Agora, usamos a regra da cadeia:
Juntando tudo temos:
Logo
Passo 3
Descobrimos que
Agora só precisamos igualar a zero para descobrirmos o máximo da função. Então temos:
mas um produto é igual a zero se e somente se, pelo menos, uma das parcelas é zero. Logo
ou
Bem, temos dois possíveis valores para . Mas qual deles é o máximo? Vamos testar!
Logo é o valor que maximiza o volume, já que para o volume é zero. E este valor está entre , que aparece na alternativa

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊