UFJF, Sem Campus, Cálculo 1, AV3 - 2018.2, Questão 6
O gráfico a seguir representa a função contínua e derivável em .
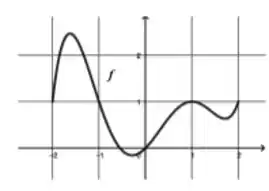
Se no intervalo representado tem pontos críticos e pontos de inflexão, então vale
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de cálculo 1. Uma bem clássica de análise de gráfico
Nosso objetivo é descobrir qual o valor de , onde são os pontos críticos e os pontos de inflexão de . Mas temos o gráfico de
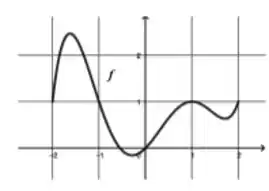
Como podemos começar? Podemos verificar os pontos críticos, né? Já que esses são os pontos onde a nossa função para de crescer e começa a decrescer e vise-versa. Então, olhando o gráfico podemos contar 4 pontos desse tipo. Ou seja,
Passo 2
Agora, podemos ver os pontos de inflexão. Esses são um pouco mais trabalhosos pois são os pontos onde a concavidade do gráfico muda. Então temos que olhar com mais calma. Da uma olhada e vê se você acha quantos pontos desses temos.
Bem, temos, ao todo, pontos de inflexão. O desenho a seguir deixa isso mais claro!
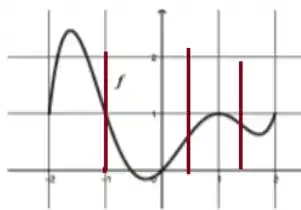
Ou seja, . E como calculamos que . Então temos que
Cujo valor está presente na alternativa
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊