Listas de Aplicações de Derivadas de Cálculo 1 da UFSC - Lista 3.5 - Máximos e Mínimos
Cálculo 1 - UFSC
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
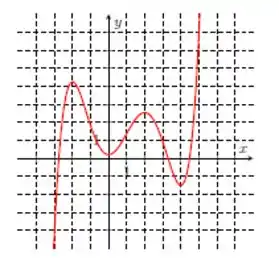
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
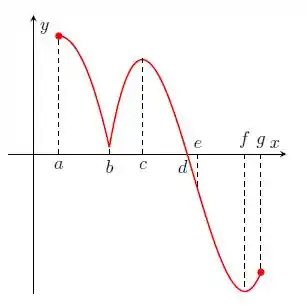
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
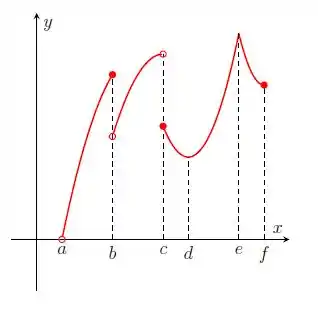
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
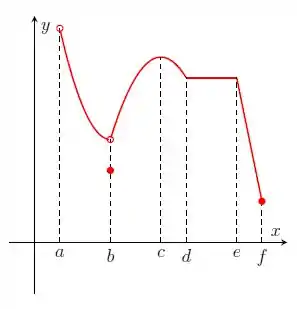
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaFaça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaFaça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaFaça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaFaça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaFaça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaFaça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaDiga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo máximo local é máximo absoluto
- Todo ponto de máximo absoluto é um ponto de máximo local
- Todo ponto de máximo locla é ponto de máximo absoluto
- Se possui máximo local, então possui máximo absoluto
- É possível que tenha infinitos pontos de máximo locais e não ter ponto de máximo absoluto
- Toda função possui máximo absoluto em um intervalo fechado
- Toda função que possui máximo absoluto em um intervalo fechado é contínua
- Se possui máximo absoluto, então possui mínimo absoluto
- Se é contínua, então possui mínimo absoluto