Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
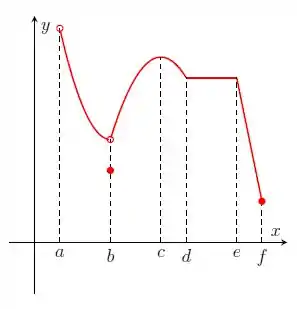
Passo 1
E aí, galerinhaaa! Bora relembrar de alguns conceitos importantes que o enunciado pede?
Primeiro, ponto crítico é aquele ponto onde a derivada será igual a zero, ou seja, ele costuma ser no local quando a reta muda de inclinação (de crescente se torna decrescente). Ponto crítico é o ponto onde isso acontece.
E quando não teremos derivada? Quando não temos uma função contínua, ou seja, a função meio que tem uma descontinuidade, e aí naquele ponto, ela não será derivável, show?
Passo 2
Olhando para nosso gráfico, podemos perceber que a função é descontínua. Como eu sei disso? Observe que tem umas bolinhas que não estão pintadas de vermelho, ou seja, elas não fazem parte do domínio da função. Os pontos críticos e números críticos são então aqueles onde temos a mudança de inclinação da nossa reta, que eu vou marcar de azul, que seria o ponto c. Mas aí você pode me perguntar, mas cara.... e ali no ponto “e”? A função tem algo que parece ser um ponto crítico!! Mas fica ligado no que diz a teoria. A teoria diz que pra ser ponto crítico a gente PRECISA MUDAR DE CRESCENTE PRA DECRESCENTE ou contrário, e, note que a função vinha em decrescente inclinação e manteve-se assim, o que garante ali não ser um ponto crítico.
Os pontos de descontinuidade, vou marcar de verde, sendo eles ponto a e b.
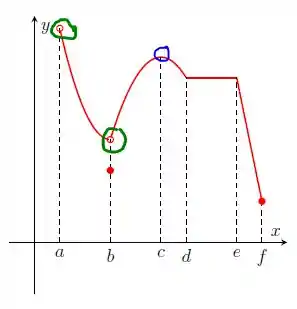
Resposta
Explicação