UFSC – Lista 3.5 – 21.1 – P2f
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Passo 1
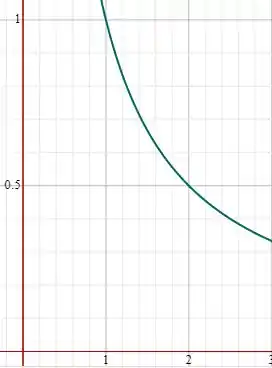
Esboçando o gráfico, ficamos com
Passo 2
Observe que no gráfico vemos um valor de máximo ali quando , onde esse valor será também 1, em outra palavras , esse é o ponto de máximo absoluto da função. Por sua vez, conforme aproximamos o valor de , , ou seja, tenderá a zero, mas nunca será zero. De forma geral, quando teremos uma assíntonta.
Resposta
Ponto de máximo absoluto igual a 1 e não há mínimo absoluto/local.
Exercícios de Livros Relacionados
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2