P1 de Física 1 - FIS1033 da PUCRIO - 2011.2

Duas esferas idênticas, uma à frente da outra, rolam sem atrito sobre um platô horizontal, com vetores velocidade iguais. A distância de separação entre elas vale e o módulo de suas velocidades vale . A seguir, elas despencam sob ação da gravidade por um plano inclinado, atingindo, ao final deste, um segundo platô horizontal em nível inferior ao primeiro (tudo ocorre sem atrito). A distância que as separa agora vale e o módulo das velocidades vale .

Em cada uma das alternativas abaixo, fazem-se duas afirmativas. Aponte a alternativa em que ambas as afirmativas estão corretas.

Obs.: As alternativas dessa questão foram alteradas em relação ao original.

1. ; A velocidade relativa entre as esferas tem mesmo módulo tanto no platô inferior quanto no superior.
2. ; A velocidade relativa entre as esferas tem módulo diferente no platô inferior em relação ao platô superior.
3. ; A velocidade relativa entre as esferas tem mesmo módulo tanto no platô inferior quanto no superior.
4. ; A velocidade relativa entre as esferas tem módulo diferente no platô inferior em relação ao platô superior.

Analise se as afirmações abaixo sobre vetores estão certas ou erradas e assinale a alternativa correta.

Obs.: Essa questão foi alterada em relação a original. Foi retirada as alternativas múltiplas escolha.

1. O trabalho realizado por uma força ao longo de um deslocamento é obtido através de um produto escalar . Onde é o ângulo entre e . Portanto, conclui-se que se a força aplicada for perpendicular ao deslocamento, o trabalho realizado será nulo.
2. O vetor torque , que expressa a tendência de um corpo sofrer ou alterar seu movimento de rotação, é dado pelo produto vetorial . Onde . O vetor é a distância do ponto de aplicação da força ao eixo de rotação e é o ângulo entre e . Portanto, é possível afirmar que o vetor torque é máximo quando os vetores e forem paralelos.
3. Um corpo estará livre de sofrer ou alterar seu movimento de rotação se a força aplicada for perpendicular à direção do vetor .

Um corpo de massa é abandonado do alto de um plano inclinado (1), que possui altura em relação ao solo, e percorre seu comprimento livre de forças de atrito até entrar em um movimento de “loop” (2), conforme mostra a figura. Use para a aceleração da gravidade.

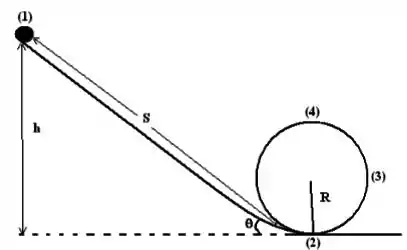
a) Utilizando um eixo de coordenadas com a direção paralela ao plano inclinado, represente o diagrama de corpo livre para a situação na qual o corpo se encontra na posição (1) e descreva, a partir da segunda lei de Newton, as componentes das forças que atuam no corpo para cada eixo.

b) Escreva a expressão para a velocidade em função da altura de lanamento com que o corpo chega à posição (2) indicada na figura.

c) Escreva a segunda lei de Newton por componentes para a situação na qual o corpo se encontra na posição (4) com velocidade e obtenha uma expressão para a altura mínima , em função do raio , de onde o corpo deve ser lançado para que consiga completar a volta no loop.

d) Considerando que o corpo abandonado de uma altura e o loop tem um raio , sua velocidade no ponto (3) é . Calcule os módulos e direções da força normal e da força resultante que atuam no corpo ao passar naquele ponto. Use .

A figura a seguir mostra o bloco () conectado a uma parede rígida por uma corda ideal, repousando sobre o bloco (). O bloco está submetido a uma força horizontal para a direita que pode variar em módulo. Adote .

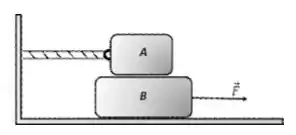
O sistema repousa sobre um solo que oferece atrito desprezível. Só existe atrito na superfície entre os blocos (). A situação inicial é de repouso.

a) Faça o diagrama de corpo livre para cada um dos blocos isoladamente. Não calcule valores, apenas nomeie todas as forças que agem em cada bloco.

b) Para o caso em que , e supondo que a corda não se rompe, calcule os vetores força de todas as outras forças que agem sobre os blocos. Use o sistema de coordenadas padrão: eixo positivo apontando para a direita, eixo positivo apontando para cima. (Dica: calcule primeiro o valor da fora de atrito estático máximo entre os blocos.)

c) Para o caso em que , calcule os módulos da aceleração do bloco e da força de tração da corda sobre o bloco , supondo que a corda não se rompe.

d) Suponha agora que a corda não exista, mas que todos os outros dados do enunciado principal sejam repetidos. Calcule o valor máximo que a força pode assumir de tal modo que não haja deslizamento relativo entre os blocos, ou seja, eles aceleram juntos.