P3 de Física 1 - FIS1033 da PUCRIO - 2011.2

Julgue os itens abaixo em verdadeiro ou falso.

I – Torque, definido por , representa uma grandeza vetorial que pode ser aplicável a uma partícula que se mova apenas em trajetórias circulares em relação a um ponto fixo, possuindo assim orientação fixa.

II – O torque possui seu valor máximo quando a força é aplicada na direção do ponto em torno do qual o corpo é capaz de sofrer rotação

III – Visto que os torques internos de um corpo rígido ocorrem aos pares (ação e reação), um corpo que sofre ação de torques externos tem seu momento angular total (definido por ) conservado.

Todas as opções são erradas

Todas as opções são corretas

Apenas a opção I é errada

Apenas a opção II é correta

Apenas a opção III é correta

Na figura abaixo são dadas duas esferas de igual massa e igual raio , porém a da esquerda é maciça (cheia) e homogênea e a esfera da direita é oca (sua massa está toda numa casca esférica de espessura desprezível).

A primeira esfera é posta para girar ao redor de um eixo deslocado de uma distância em relação a um de seus diâmetros. É possível, nestas condições, a segunda esfera apresentar um momento de inércia de valor aproximadamente igual ao da primeira?

Não, a esfera cheia apresenta maior momento de inércia que a oca já no caso , e deslocar o eixo para longe do centro de massa só iria aumentar seu momento de inércia.

Sim, mas só quando

Sim, mas só quando

Sim, mas só quando

Sim, mas só quando

A figura mostra uma haste homogênea vertical articulada por um parafuso , preso em sua extremidade superior e que oferece atrito desprezível. A haste tem massa e comprimento . Uma bola de neve de massa viaja em direção à haste e vai atingi-la exatamente em seu centro. No momento da colisão da bola de neve é dada pelo vetor (ver figura para o sistema de coordenadas).

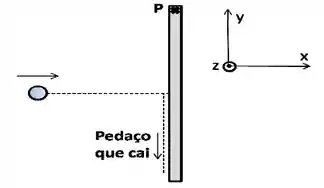
Como resultado da colisão, a bola se parte em três pedaços de igual massa . O pedaço se gruda à haste, o pedaço se solta, caindo inicialmente com velocidade , e o pedaço sai com velocidade .

Calcule, em relação ao ponto P, o vetor momento angular total do sistema antes da colisão, sabendo que a haste se encontra inicialmente em repouso. Responda ainda se haverá ou não conservação do momento angular total do sistema na colisão, justificando cuidadosamente.

Calcule, em relação ao ponto P, os vetores momentos angulares e dos pedaços e logo após a colisão.

Determine o momento de inércia do conjunto haste pedaço .

Calcule a velocidade angular da haste após a colisão e também a energia cinética de rotação do conjunto haste pedaço .

Um sistema é composto por uma haste de massa e comprimento , que está livre para girar em torno de um eixo que passa pelo seu centro de massa, e por duas massas pontuais e , que se encontram afixadas nas extremidades da haste, conforme mostra a figura. Inicialmente, haste e massa estão em repouso na direção horizontal, quando são liberadas e passam a exercer rotações em torno do eixo no sentido horário. Despreze os efeitos e resistências do ar.

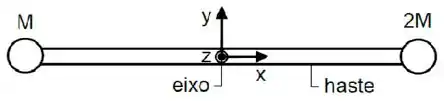
Determine as coordenadas e do centro de massa do sistema para a situação descrita.

Determine o momento de inércia de rotação associado ao sistema.

Determine o vetor torque em relação ao eixo de rotação exercido pela força peso de cada componente do sistema e o vetor torque resultante, indicando sua direção em termos dos vetores unitários de base, conforme indicado na figura.

Utilizando conceitos de energia e seu princípio da conservação, determine a velocidade angular de rotação do sistema ao passar pela posição vertical. Poderíamos também utilizar as expressões da cinemática rotacional para calcular a velocidade angular? Justifique.