Corpos Rígidos, Dinâmica de Rotação, Momento Angular
A figura mostra uma haste homogênea vertical articulada por um parafuso , preso em sua extremidade superior e que oferece atrito desprezível. A haste tem massa e comprimento . Uma bola de neve de massa viaja em direção à haste e vai atingi-la exatamente em seu centro. No momento da colisão da bola de neve é dada pelo vetor (ver figura para o sistema de coordenadas).
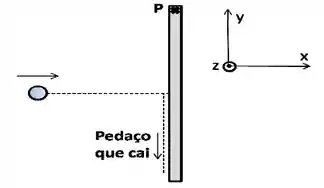
Como resultado da colisão, a bola se parte em três pedaços de igual massa . O pedaço se gruda à haste, o pedaço se solta, caindo inicialmente com velocidade , e o pedaço sai com velocidade .
Calcule, em relação ao ponto P, o vetor momento angular total do sistema antes da colisão, sabendo que a haste se encontra inicialmente em repouso. Responda ainda se haverá ou não conservação do momento angular total do sistema na colisão, justificando cuidadosamente.
Calcule, em relação ao ponto P, os vetores momentos angulares e dos pedaços e logo após a colisão.
Determine o momento de inércia do conjunto haste pedaço .
Calcule a velocidade angular da haste após a colisão e também a energia cinética de rotação do conjunto haste pedaço .
Passo 1
Para calcular o momento angular total do sistema antes, vamos relembrar a definição de momento , , agora, mão na massa!
Para o sistema, temos:
O momento angular da haste é zero, pois a força peso atua na direção do eixo, portanto, não produz torque.
Passo 2
Agora que já lembramos da definição de momento angular, podemos calcular o momento angular dos pedaços após a colisão, se liga!
Para o pedaço , temos:
O produto vetorial dá zero pois os vetores apontam na mesma direção!
Passo 3
Para o pedaço , temos:
A direção e o sentido do vetor podem ser determinados pela regra da mão direita!
Passo 4
Agora vamos determinar o momento de inércia do conjunto:
Passo 5
Para calcular a velocidade angular do conjunto depois da colisão, podemos recorrer à conservação do momento angular, vamos lá!
Como calculamos o momento angular antes da colisão no item a, e os momentos angulares dos pedaços e , e só substiruir!
Sabemos, que como o conjunto haste1 é um corpo rígido, temos:
Como já calculamos o momento de inércia do conjunto, fica:
A energia cinética do conjunto haste + pedaço 1 vai ser
Já calculamos tudo isso! Agora é só jogar os valores
Resposta
a)
b)
c)
d)