Sistema de Partículas, Corpos Rígidos, Energia Potencial e Conservação da Energia Mecânica, Dinâmica de Rotação
Um sistema é composto por uma haste de massa e comprimento , que está livre para girar em torno de um eixo que passa pelo seu centro de massa, e por duas massas pontuais e , que se encontram afixadas nas extremidades da haste, conforme mostra a figura. Inicialmente, haste e massa estão em repouso na direção horizontal, quando são liberadas e passam a exercer rotações em torno do eixo no sentido horário. Despreze os efeitos e resistências do ar.
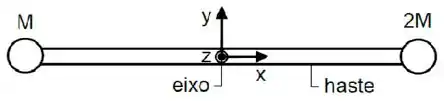
Determine as coordenadas e do centro de massa do sistema para a situação descrita.
Determine o momento de inércia de rotação associado ao sistema.
Determine o vetor torque em relação ao eixo de rotação exercido pela força peso de cada componente do sistema e o vetor torque resultante, indicando sua direção em termos dos vetores unitários de base, conforme indicado na figura.
Utilizando conceitos de energia e seu princípio da conservação, determine a velocidade angular de rotação do sistema ao passar pela posição vertical. Poderíamos também utilizar as expressões da cinemática rotacional para calcular a velocidade angular? Justifique.
Passo 1
Para determinar as coordenadas do centro de massa, vamos primeiro lebrar da definição! Ah...como a barra está na horizontal, sobre o eixo , o centro de massa não terá componente no eixo , portanto:
Agora sim vamos calcular a componente !
Para nosso sistema, temos:
Passo 2
Vamos agora calcular o momento de inércia do sistema! Lembrando que o eixo de rotação passa pelo centro de massa da barra, que é no meio da barra.
Passo 3
Para calcular o torque resultante, vamos calcular o torque de cada componente em relação ao eixo de rotação:
O torque da haste é zero, pois a força peso atua exatamente no eixo, ou seja, o vetor é zero!
Passo 4
Vamos agora calucular o vetor torque das massas e !
Para a massa , temos:
Passo 5
Agora que temos os três vetores torque em separado, podemos fazer a soma para descobrir o vetor resultante! Se liga!
Passo 6
Para calcular a velocidade angular quando o sistema passa pela posição vertical, precisamos lembrar o princípio de conservação da energia, para o sistema, temos que soma da variação da energia cinética rotacional com a variação da energia potencial gravitacional, deve ser zero!
Vamos determinar cada variação de energia!
Passo 7
Para a energia cinética, temos:
Como o sistema parte do repouso:
Para a energia potencial, adotando , como potencial zero, temos que a energia potencial no início é zero, mas quando o sitema fica na vertical, temos:
Passo 8
Agora sim, podemos substituir na fórmula da conservação!
Isolando , e substituindo o momento de inércia pelo valor que achamos no item b, temos:
Infelizmente a cinemática rotacional seria de pouco uso, pois no caso desse sistema, temos uma aceleração variável. O movimento circularmodela sistemas com aceleração constante.
Resposta
;
; Não, o sistema possui aceleração variável, que seria de difícil modelagem na cinemática rotacional.