P3 de Física 1 - FIS1033 da PUCRIO - 2013.2

Uma roldana maciça e homogênea tem seu eixo central fixo e pode ser solicitada a girar por cordas presas tanto a seu raio interno , quanto a seu raio externo . A peça toda é rígida.

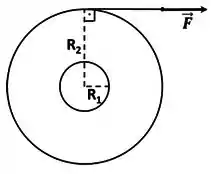
Uma força de módulo constante igual a e direção sempre perpendicular ao raio externo da roldana a acelera desde o repouso até o instante em que sua velocidade angular vale . Durante essa rotaçãoo, o deslocamento angular da roldana é de 3,2 rad. Usando que , calcule o momento de inércia da roldana.

Calcule a potencia instantenea desenvolvida pela força no instante considerado no item .

Uma roldana maciça e homogênea tem seu eixo central fixo e pode ser solicitada a girar por cordas presas tanto a seu raio interno , quanto a seu raio externo . A roldana sustenta por seu raio interno um corpo de massa , e está atrelada, por seu raio externo, a uma mola de constante elástica . O sistema está inicialmente em repouso com a mola destendida de .

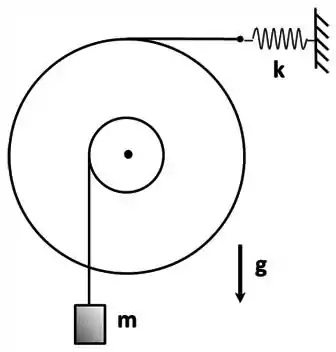
) O sistema é liberado e num determinado instante a distensão da mola vale de . Calcule a variação da altura do corpo desde que o sistema foi liberado até este instante, respondendo se o corpo subiu ou desceu.

) Calcule a velocidade angular da roldanano instante considerado no item . Considere que a variação de altura do corpo é de , que o momento de inércia da roldana vale e

Um cabo ideal está enrolado em volta de uma polia de raio e massa e tem sua outra extremidade ligada a um bloco de . O bloco se encontra apoiado sobre um plano inclinado de em relação a horizontal. O sistema é solto a partir do repouso. Não existe atrito entre o plano e o bloco. Considerando o momento de inércia da polia calcule:

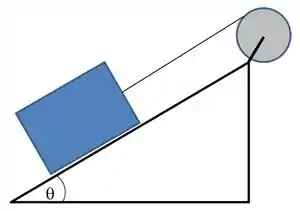
A aceleração angular da polia.

a tração no cabo e o torque na polia.

O módulo da aceleração linear de um ponto na borda na polia após de iniciado o movimento.

Duas esferas de são presas às extremidade de uma barra fina de massa desprezível, de de comprimento. A barra pode girar livremente, sem atrito, num plano vertical, em torno de um eixo horizontal que passa pelo seu centro. Enquanto a barra está na horizontal como mostra afigura, uma massinha de cai com velocidade de sobre uma das esferas e fica grudada a ela. Considerando as esferas como massa pontuais, calcule:

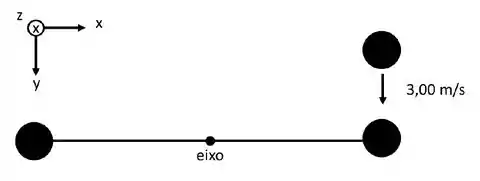
O momento de inércia do sistema em torno do eixo após a colisão.

A velocidade angular do sistema imediatamente após a colisão.

O vetor torque resultante realizado pela força peso no sistema quando a barra faz uma ângulo de com a horizontal.

Qual será o ângulo medido a partir da horizontal em que o sistema irá parar temporariamente.