Uma roldana maciça e homogênea tem seu eixo central fixo e pode ser solicitada a girar por cordas presas tanto a seu raio interno , quanto a seu raio externo . A peça toda é rígida.
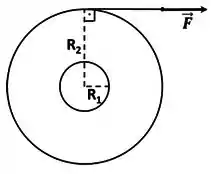
Uma força de módulo constante igual a e direção sempre perpendicular ao raio externo da roldana a acelera desde o repouso até o instante em que sua velocidade angular vale . Durante essa rotaçãoo, o deslocamento angular da roldana é de 3,2 rad. Usando que , calcule o momento de inércia da roldana.
Calcule a potencia instantenea desenvolvida pela força no instante considerado no item .
Passo 1
Para resolver o item a, eles já nos forneceram uma das fórmulas, , show! Mas a gente vai precisar lembrar, que para esse caso da roldana, onde ela está apenas girando, ela terá somente energia cinética de rotação . E por causa disso, podemos dizer que . Sacou!? Então vamos lá!
Ou seja:
Agora é só substiruir os valores para achar !
Passo 2
Todos os valores foram dados no enunciado, basta lembrar que como ele disse que a roldana parte do repouso, temos que a velocidade angular inicial é zero! Agora sim, vamos substituir! Ahh...não se esqueça de usar o S.I!
Passo 3
Para calcular a potência, precisamos de uma fórmula que relacione potência com as grandezas angulares, Ah...é só usar, ! Então vamos lá!
Resposta