Corpos Rígidos, Rotação, Dinâmica de Rotação, Momento Angular, Trabalho e Energia Cinética
Duas esferas de são presas às extremidade de uma barra fina de massa desprezível, de de comprimento. A barra pode girar livremente, sem atrito, num plano vertical, em torno de um eixo horizontal que passa pelo seu centro. Enquanto a barra está na horizontal como mostra afigura, uma massinha de cai com velocidade de sobre uma das esferas e fica grudada a ela. Considerando as esferas como massa pontuais, calcule:
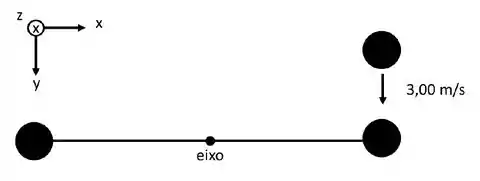
O momento de inércia do sistema em torno do eixo após a colisão.
A velocidade angular do sistema imediatamente após a colisão.
O vetor torque resultante realizado pela força peso no sistema quando a barra faz uma ângulo de com a horizontal.
Qual será o ângulo medido a partir da horizontal em que o sistema irá parar temporariamente.
Passo 1
Vamos calcular o momento de inércia, para isso precisamos lembrar da fórmula!
Onde é a distância da massa até o eixo. No nosso caso, temos três corpos, as massas pontuais. Para elas, o momento de inércia fica;
Passo 2
Para calcular a velocidade angular após a colisão, iremos recorrer à conservação do momento angular, . Se liga! Antes da colisão, a barra estará em repouso, logo não irá contribuir, mas a massinha que está caindo irá! Depois da colisão, a barra como um todo, agora que a massinha grudou na esfera, irá girar em torno de seu eixo, desse modo, temos:
Passo 3
Agora é só substituir, já temos todos os valores, inclusive o momento de inércia, pois já o calculamos no item !
Passo 4
Para achar o vetor torque, basta lembrar da definição de torque,, agora é só usar a fórmula, mas é sempre com fazer um desenho para ter uma ideia melhor do que estamos fazendo!
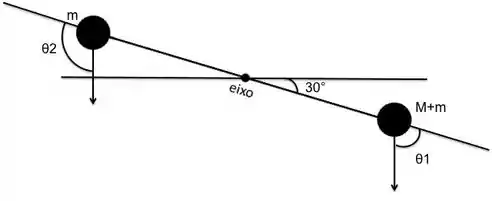
Passo 5
Agora que temos a figura, fica mais fácil, vamos lá! Para achar os ângulos é só usar trigonometria básica que você não vai errar!
Opaa...de onde surgiu essa direção e sentido do vetor torque!? Bom usando a regra da mão direita, encontramos que o vetor torque aponta para dentro do papel, e de acordo com o eixo que o enunciado indica, sabemos que é positivo para a coordenada , e portanto deve ser ! Sacou!?
Passo 6
Para descobrir quando o sistema irá parar temporariamente, devemos recorrer ao teorema do trabalho e energia cinética, , onde o trabalho é igual a variaçãoo da energia cinética. E para rotação, fica:
ou seja:
Sabemos que e que , então, temos:
Resposta