Força e Leis de Newton, Corpos Rígidos, Energia Potencial e Conservação da Energia Mecânica, Rotação
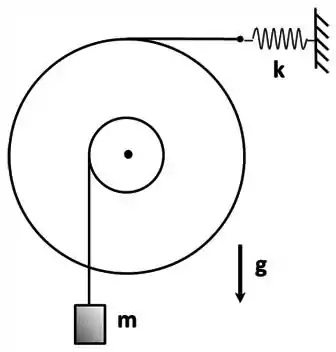
Uma roldana maciça e homogênea tem seu eixo central fixo e pode ser solicitada a girar por cordas presas tanto a seu raio interno , quanto a seu raio externo . A roldana sustenta por seu raio interno um corpo de massa , e está atrelada, por seu raio externo, a uma mola de constante elástica . O sistema está inicialmente em repouso com a mola destendida de .
) O sistema é liberado e num determinado instante a distensão da mola vale de . Calcule a variação da altura do corpo desde que o sistema foi liberado até este instante, respondendo se o corpo subiu ou desceu.
) Calcule a velocidade angular da roldanano instante considerado no item . Considere que a variação de altura do corpo é de , que o momento de inércia da roldana vale e
Passo 1
Considerando que o corpo parte do repouso, onde a mola está distendida de , para uma situação onde a mola apresenta uma distensão de , sabemos que a roldana girou no sentido horário. Ou seja, o corpo subiu, então vamos calcular quanto!
Passo 2
Agora, vamos descobrir quantos radianos a roldana girou para que a mola encolhesse :
Usando os valores informado, temos:
Como a roldana é uma peça rígida, o raio interno também girou no sentido horário, vamos agora descobrir quanto o corpo subiu!
Passo 3
Para determinar a velocidade angular da roldana, devemos recorrer à Lei da Conservação da Energia Mecânica:
No início, temos apenas energia potencial elástica, pois estou considerando que o bloco está na origem do potencial gravitacional.
No fim, temos energia pontencial elástica, energia potencial gravitacional do bloco, que subiu, além de ter a energia cinética do bloco, que possui velocidade para cima, assim como energia cinética de rotação da roldana, que está girando!
Como o bloco está atrelado ao raio interno, podemos dizer que !
Passo 4
Substituindo os valores, temos:
Isolando a velocidade angular, temos:
Resposta