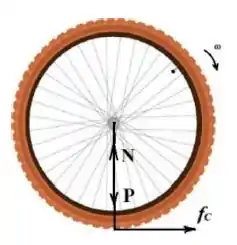
Considere uma roda de massa , raio e momento de inércia girando com velocidade angular inicial , sentido horário, baixada sobre uma superfície plana horizontal rugosa com seu centro de massa em repouso inicialmente. O coeficiente de atrito cinético entre a roda e o plano é . A seguir a roda se move no sentido positivo do eixo , deslizando e girando durante um intervalo de tempo . Após o instante de tempo , segue rolando sem deslizar.
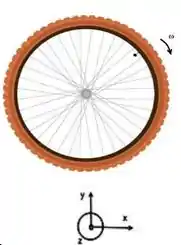
Indique no desenho, as forças que agem sobre a roda durante . Determine na forma literal uma expressão para o coeficiente de atrito cinético em função dos dados citados.
Passo 1
Temos 3 forças aqui: a força peso, normal e o atrito cinético (pois a roda desliza). As forças estão apontadas abaixo
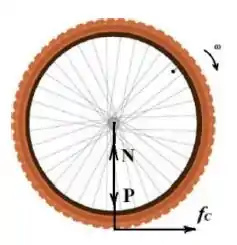
Passo 2
Primeiramente temos que a roda não realiza movimentos na direção assim temos que
E o atrito cinético, no intervalo de tempo , é dado por
Passo 3
Na direção temos que a força resultante é a força de atrito, ou seja
Beleza! O problema é que a aceleração não nos foi dada! Então temos que relacionar com os dados do problema.
Vamos ver o que eu tenho aqui... momento de inércia, raio, velocidade angular inicial, massa, intervalo de tempo ... um montão de coisas! E como a gente relaciona isso tudo?!
Bem, podemos começar a falar de rotações, já que temos momento de inércia, raio e essas coisas.
Passo 4
O nosso atrito cinético só aparece durante no intervalo de tempo .
Como a roda desliza não podemos usar !
O que sabemos aqui é que esse atrito exerce um torque sobre a roda
E esse atrito está no sentido contrário da velocidade angular da roda, ou seja, causa uma desaceleração angular dada por
Nesse intervalo a nossa roda sofre uma mudança de velocidade angular dada por . Como antes desse intervalo a velocidade angular era e depois desse intervalo essa velocidade angular volta a ficar constante e é dada por , temos
Agora só falta esse !!! Caaalllllmaaa! Tamo chegando já! Vem comigo o/
Passo 5
Pra achar esse , agora podemos usar a condição de não-deslizamento!
Onde é a velocidade do centro de massa da roda (movimento de translação). No intervalo de tempo temos que o centro de massa da nossa roda está em um movimento acelerado devido à força de atrito!
Sim! Ela está aumentando a velocidade de translação e diminuindo a velocidade de rotação!
Nesse intervalo de tempo a velocidade aumentou
Essa aceleração já calculamos lá no começo! Assim temos
Pelo enunciado temos que essa velocidade inicial é nula, ou seja
Assim finalmente chegamos em
Passo 6
Agora podemos finalmente juntar tudo!
Partimos de
E usamos que
Assim
Isolando
E tadááááá! Deu trabalho mas ficou lindão no final :)
Resposta
Diagrama de forças