A figura mostra um sistema mecânico simples. Uma haste delgada de massa e comprimento está presa em uma extremidade por um pino e livre para girar sem atrito. Na outra extremidade se encontra presa uma esfera de massa e raio desprezível. Considere e a distância vertical
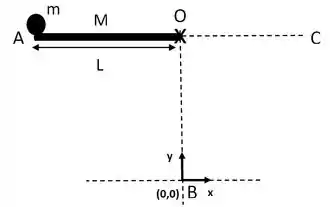
Dados:
-
-
-
-
Determine
- Uma expressão literal para o momento de inércia do sistema em relação ao ponto fixo , contendo somente as variáveis indicadas no enunciado.
- Um valor numérico para este momento de inércia.
- O momento angular total do sistema ao passar pelo ponto B.
Passo 1
Temos que o momento de inércia total será dado por
O momento de inércia da massa é dado simplesmente por
No caso da haste temos que lembrar que o seu centro de massa não está sobre o eixo de rotação, assim temos que usar o teorema dos eixos paralelos.
Onde é a distância do centro de massa da haste até o eixo de rotação.
Pela figura vemos que
Assim
E agora temos o momento de inércia total!
Passo 2
Agora só temos que substituir os valores numéricos
Passo 3
Temos que utilizar a conservação de energia mecânica.
No começo temos somente energia potencial gravitacional da barra e da massa
Quando a extremidade da barra passar pelo ponto teremos energia cinética de rotação do sistema e energia potencial gravitacional da barra, já que o seu centro de massa (que é no meio da barra) está a uma altura .
Assim
Assim, usando a conservação de energia mecânica
Passo 4
Agora podemos calcular o momento de inércia usando
Resposta
(A)
(B)
(C)