Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Não-Ideais

Ver Teoria
Exercício 2112345678910111213141516171819202223242526272829303132333435363738394041424344454647

Enunciado

Um bloco de massa m encontra-se suspenso por uma corda ideal que passa por uma roldana de raio r , com momento de inércia I . A corda encontra-se enrolada ao cilindro central de um carretel na outra extremidade. O bloco é liberado a partir do repouso. A roldana e o carretel podem girar livremente (sem atrito) em torno de seus eixos fixos. Os centros de massa dos carretéis estão em repouso, não transladam.

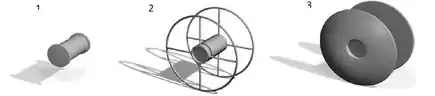
  1. Considere os três carretéis abaixo feitos de materiais diferentes, com formas diferentes, de modo a terem a mesma massa. As distribuições de massa são homogêneas nas partes sólidas. Os três carretéis possuem o mesmo cilindro central. Com qual dos carretéis o bloco teria o menor valor da aceleração? Justifique sua resposta.

  2. Calcule o momento de inércia do carretel n º 2 , considerando que cada uma das hastes é delgada, tem massa 𝑀 e comprimento 3 R / 4 . Os anéis são finos com massa 𝑀 e raio 𝑅. O cilindro central possui massa M e raio R / 4 .
  3. Sabendo-se que o carretel utilizado foi o n º 2 . Qual a aceleração adquirida pelo bloco durante sua queda? Admita g = 9,81   m / s 2 , M =   5,00 × 10 - 1 K g , m = 3,00   k g , R =   1,00   m , r = 1,00 × 10 - 1 m e I = 5,00 × 10 - 3 k g . m 2 .

Passo 1

Temos que a corda exercerá um torque de mesma intensidade sobre os três carretéis, já que o fio está enrolado no cilindro interno (que tem mesmas dimensões para cada carretel) de cada um.

Temos que a segunda lei de Newton para rotações é dada por

τ → = I α →

Assim, quanto maior o momento de inércia menor será a aceleração angular no corpo, então temos que saber qual dos carretéis acima tem maior momento de inércia.

Para isso temos que lembrar que o momento de inércia é dado por

I = ∫ d m   r 2

Ou seja, quanto mais afastado do eixo de rotação for a distribuição de massas de um dado objeto maior será o seu momento de inércia.

Vemos que o primeiro tem toda sua massa concentrada no cilindro menor, logo, esse cara vai ser o que tem menor momento de inércia!

No terceiro temos que parte da massa está distribuída em torno dos círculos maiores enquanto que no segundo parte dessa massa está concentrada em anéis.

Assim quem tem maior momento de inércia será o carretel 2 .

Passo 2

Temos que o carretel 2 tem 8 dessas hastes, 2 anéis de raio R e um cilindro de raio R / 4 , assim o seu momento de inércia total será dado por

I 2 = 8 I h a s t e + 2 I a n e l + I c i l i n d r o

Provavelmente esses momentos de inércia estarão no seu formulário!

O momento de inércia de uma haste de comprimento L é dado por I = M L 2 / 12 . A nossa haste tem comprimento 3 R / 4 e massa M .

Porém, temos que lembrar de uma coisa mega ultra super importante!!!!!

O centro de massa da nossa haste não está localizado no eixo de rotação! Nesse caso temos que usar o teorema dos eixos paralelos! O momento de inércia será dado por

I h a s t e ' = I h a s t e + M d 2

Onde d é a distância entre o centro de massa da haste e o centro de rotação. Como o centro de massa está no centro da haste (que é homogênea) e sua extremidade mais próxima do centro de rotação está a uma distância de R / 4 do centro de rotação, temos que

d = 1 2 3 R 4 +   R 4 = 5 R 8

Assim o momento de inércia da haste é dado por

I h a s t e ' = I h a s t e + M d 2 = M R 2 12 + M 5 R 8 2

I h a s t e ' = 7 16 M R 2

O momento de inércia de um anel de raio R e massa M é dado por

I a n e l = M R 2

O momento de inércia de um cilindro de raio r é dado por I = M r 2 / 2 . Como nosso cilindro tem raio R / 4 e massa M

I c i l i n d r o = 1 2 M R 4 2 = M R 2 32

Assim, juntando tudo temos

I 2 = 8 × 7 16 M R 2 + 2 M R 2 + M R 2 32

I 2 = 177 32 M R 2 = 5,53 M R 2

Passo 3

Temos a situação da figura a seguir

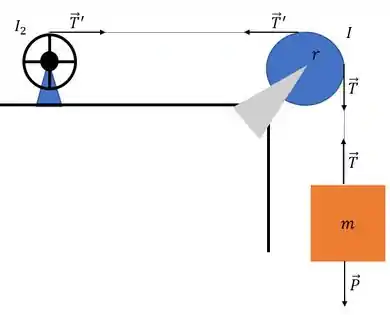
Onde eu já apontei todas as forças relevantes (omiti as forças que os suportes exercem sobre a roldana e o carretel e os seus pesos, pois essas forças não exercem torque – apontam na direção do centro de rotação).

Passo 4

Queremos achar a aceleração do bloco que vai ser influenciada pelas acelerações angulares do carretel e da polia!

Primeiramente vamos escrever as equações de movimento

- Bloco

Pela segunda lei de Newton

m a = m g - T

Guarda ela aí!

Passo 5

- Roldana

Temos dois torques atuando: um da tensão T → ' e outro da tensão T → ! Assim o torque total é dado por

τ = T r - T ' r

Onde eu adotei o sentido horário como positivo (ou seja, no sentido de queda do bloco).

Por outro lado, temos que o torque se relaciona com o momento de inércia por

τ = α I

E a aceleração angula se relaciona com a aceleração linear por

a = α r → α = a r

Juntando tudo isso temos

τ = α I = a I r

E

a I r = T r - T ' r

Beleza, guarda mais essa aí!

Passo 6

- Carretel

Sobre o carretel temos somente uma força exercendo torque

τ 2 = T ' R

Lembrando que o carretel tem raio R !

Usando a segunda lei para rotações

τ 2 = α 2 I 2

Relacionando as acelerações angular e linear

a = α 2 R → α 2 = a R

Juntando tudo temos

τ 2 = α 2 I 2 = a R I 2

a R I 2 = T ' R

Passo 7

Temos o seguinte sistema de equações

m a = m g - T a I r = T r - T ' r a R I 2 = T ' R

Isolando T ' na terceira equação, temos

T ' = a R 2 I 2

Onde podemos substituir na segunda equação

a I r = T r - T ' r

a I r = T r - a R 2 I 2 r

Agora podemos isolar a tensão T

T r = a I r + a R 2 I 2 r

T = a I r 2 + a I 2 R 2

T = a I r 2 + I 2 R 2

Agora só falta substituir na primeira equação!!!

m a = m g - T

m a = m g - a I r 2 + I 2 R 2

m a + a I r 2 + I 2 R 2 = m g

Dividindo toda a equação por m

a + a I m r 2 + I 2 m R 2 = g

a 1 + I m r 2 + I 2 m R 2 = g

a = g 1 + I m r 2 + I 2 m R 2

Show!!!! Agora é só substituir os valores do enunciado e o I 2 achado no item anterior ;)

g = 9,81   m / s 2 , M =   5,00 × 10 - 1 K g , m = 3,00   k g , R =   1,00   m , r = 1,00 × 10 - 1 m e I = 5,00 × 10 - 3 k g . m 2

a = 9,81 1 + 5 × 10 - 3 3 × 10 - 1 2 + 5,53 × 5 × 10 - 1 × 1 2 3 × 1 2

a = 0,616   m / s 2

Resposta

(A) Carretel 2 , pois tem maior momento de inércia

(B) I 2 = 177 32 M R 2 = 5,53 M R 2

(C) a = 0,616   m / s 2  

Exercícios de Livros Relacionados

Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,