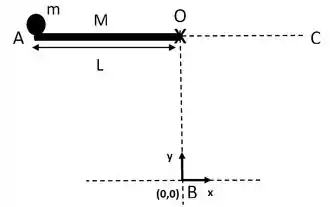
A figura mostra um sistema mecânico simples. Uma haste delgada de massa e comprimento está presa em uma extremidade por um pino e livre para girar sem atrito. Na outra extremidade se encontra presa uma esfera de massa e raio desprezível. Considere e a distância vertical
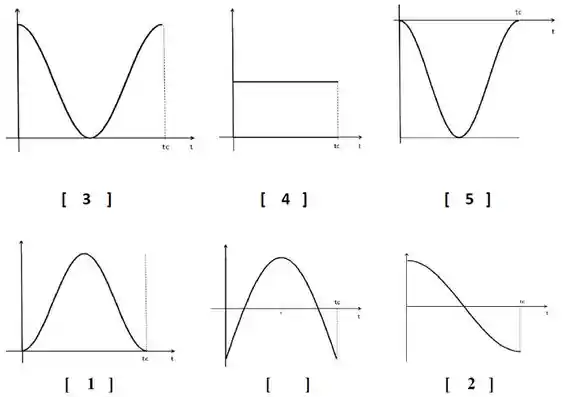
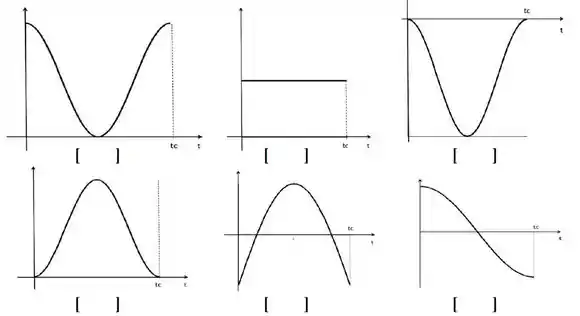
Considere agora o movimento do sistema abandonado do repouso no ponto A. Indique com o número apropriado o gráfico que representa cada uma das grandezas físicas do movimento em função do tempo até que o sistema finalmente alcance novamente o repouso no ponto C.
[1] O Momento Angular Total do Sistema.
[2] O Torque que Atua no Sistema
[3] A Energia Potencial Gravitacional.
[4] A Energia Mecânica Total
[5] A variação da Energia Potencial Gravitacional.
Passo 1
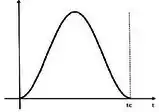
[1] – Temos que inicialmente que não há velocidade angular, ou seja, o momento angular inicialmente é nulo.
A partir do momento em que a barra é solta, ela vai ganhando velocidade angular, até bater um valor máximo passando pelo ponto e depois essa velocidade angular diminui até quando a barra volta a ficar horizontal (chegando ao ponto ).
O gráfico que melhor representa o momento angular é o
Passo 2
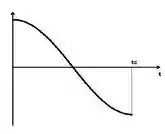
[2] – Temos que o torque é dado por
Outra forma de escrever seria
Quando a barra está no ponto temos que , ou seja
Quando a barra está no ponto temos que, ou seja
Quando a barra está no ponto temos que, ou seja
O gráfico que melhor representa esse comportamento é o
Passo 3
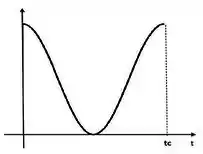
[3] – A energia potencial gravitacional por
Nos pontos e essa energia potencial gravitacional vale e no ponto vale . Assim o gráfico que melhor representa esse comportamento é
Passo 4
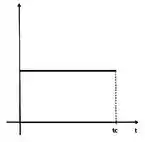
[4] – Temos que a energia mecânica tem que conservar, ou seja, ela é constante com o tempo!
Passo 5
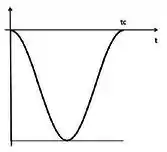
[5] – A variação de energia potencial gravitacional é dada por
Onde é a energia potencial gravitacional inicial (energia potencial no ponto ). Assim temos que
Nos pontos e essa diferença de energia é e no ponto (onde essa diferença de energia é . O gráfico que melhor representa esse comportamento é
Resposta