Considere o carrossel, da figura abaixo, como um disco de massa e raio . As barras horizontais são finas, têm massa e comprimento . As barras verticais também são finas, possuem massa e altura . O eixo central é constituido por um cilindro de massa e raio desprezíveis.

Dados:
Disco: ;
Haste: ;
;
(a) Calcule o momento de inércia desse carrossel em relação ao eixo central vertical (CM).
Passo 1
Eita, momento de inércia dessa figura complicada...
Calma, é só a gente separar cada elemento que fica mais fácil de calcular isso aí.
Queremos calcular o momento de inércia com relação a um eixo vertical passando no centro de carrossel:
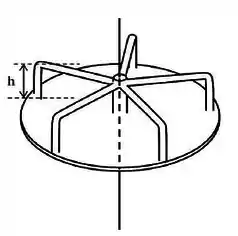
O carrosel vai ser composto pelo disco central (base), por barras verticais e por barras horizontais.
Então, seu momento de inércia será a soma dos momentos de inércia de tudo isso aí:
Passo 2
Vamos começar calculando o momento de inércia do disco da base do carrossel .
No formulário ele nos dá a expressão para o momento de inércia de um disco com relação ao eixo que passa perpendicularmente em seu centro de massa:
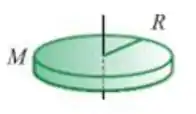
É exatamente isso que precisamos.
Então, é só aplicar essa fórmula para a massa do disco e seu raio :
Substituindo os valores, temos:
Passo 3
Vamos às barras verticais.
Como a barra é fina, seu raio é desprezível.
Então, todos os elementos de massa da barra estão a uma mesma distância do eixo central:
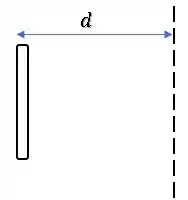
Logo, podemos calcular o momento de inércia com aquela mesma fórmula de momento de inércia para partículas.
A ideia é que podemos pensar na barra como vááááárias partículas à uma mesma distância do eixo de rotação. Cada uma delas tendo seu momento de inércia calculado com:
A soma de todos esse momentos de inércia seria o momento de inércia da barra:
Onde é igual ao raio do carrossel:
Substituindo:
Passo 4
Por último, temos as barras horizontais.
Essa é a mais chatinha dos três elementos, mas fique tranquilo que não é nada demais.
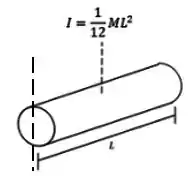
Sabemos calcular o momento de inércia de uma barra fina com relação a um eixo passando transversalmente pelo seu centro:
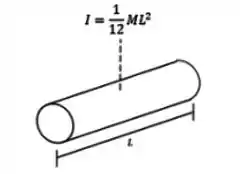
Esse seria o momento de inércia de uma haste no formulário:
Porém, temos que calcular o momento de inércia com relação ao eixo passando pela sua extremidade:
Então, vamos aplicar o teorema dos eixos paralelos:
Onde é a distância entre os eixos, correspondente a metade do comprimento da barra.
O comprimento da barra horizontal é :
Substituindo o valor de massa:
Passo 5
Pronto, agora é só juntar tudo na expressão do momento de inércia total do carrossel:
Resposta
(a)