Considere agora um disco horizontal de raio com quatro hastes conforme a figura ao lado. NÃO é o carrossel do item anterior. Duas pessoas empurram esse disco no sentido anti-horário. Veja a figura abaixo com vista de cima. A força de cada pessoa tem módulo constante , sendo tangente à borda. Não há atrito entre o eixo central e o disco. O sistema disco-hastes tem momento de inércia .

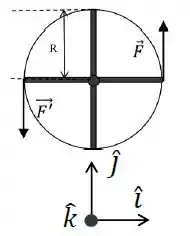
(b) Calcule a aceleração angular do sistema disco-hastes.

O torque resultante será a soma dos torques de todas as forças externas sobre o objeto:

OBS: O disco está apoiado sobre o eixo central, logo, as forças peso e normal não geram torque com relação ao eixo central. Além disso, não há atrito.

O torque da força será:

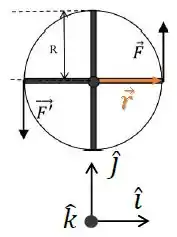
Como os vetores são perpendiculares, o módulo do torque será:

Mas queremos a direção e o sentido do vetor também.

Com a regra da mão direita, temos os dedos indicadores apontados para a direita na direção de e a palma da mão voltada para cima na direção de . Ao fechar os dedos na direção de , nosso dedão aponta para cima na direção .

Então, nosso vetor torque é:

O torque da força será:

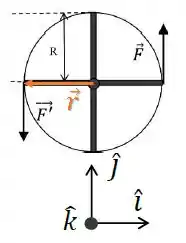
Assim como no outro caso, os vetores são perpendiculares, seu módulo também será:

Com a regra da mão direita, temos os dedos indicadores apontados para a esquerda na direção de e a palma da mão voltada para baixo na direção de . Ao fechar os dedos na direção de , nosso dedão aponta para cima na direção .

Então, assim como o outro vetor torque, o torque da força será:

Isso acontece pois as forças são iguais, as distâncias ao eixo de rotação são as mesmas e ambas tentam fazer o objeto rodar no sentido anti-horário. Assim, seus torques são os mesmos.

O torque resultante será:

Substituindo na segunda lei de Newton para rotação, temos:

O vetor aceleração angular tem a mesma direção e o mesmo sentido do vetor torque:

Substituindo os valores: