Uma esfera maciça em repouso está sobre um plano inclinado e possui uma fita ideal enrolada em torno de sua periferia vertical. Essa fita passa em polia ideal e está ligada a um bloco. Veja figura. Após liberar o conjunto, a esfera sobe o plano sem deslizar e o bloco desce.
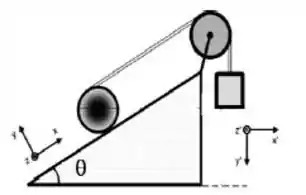
Encontre uma expressão literal para o módulo da aceleração do CM da esfera e da aceleração do bloco. São dados o raio da esfera 𝑅, o ângulo 𝜃, as massas da esfera 𝑀 e do bloco 𝑚 e a aceleração da gravidade 𝑔. A aceleração da fita no ponto superior da esfera é duas vezes a aceleração do CM da esfera.
Dados: Esfera:
(a) Escreva a equação do movimento para o bloco acompanhada do respectivo diagrama de corpo livre.
(b) Escreva a equação do movimento de translação da esfera acompanhada do respectivo diagrama de corpo livre. Faça o mesmo para a equação do movimento de rotação da esfera. Escreva também a condição de rolamento sem deslizamento.
(c) Resolva o sistema de equações e encontre uma expressão literal para o módulo da aceleração do CM da esfera em função dos dados fornecidos.
Passo 1
Vamos resumir isso ai...
A figura é essa:
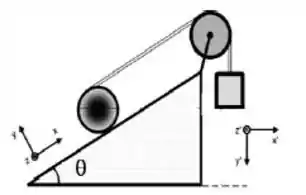
O bloco desce e a esfera sobe sem deslizar no plano.
Nossos dados são esses:
Além disso é dado que a aceleração da fita é duas vezes a aceleração do centro de massa da esfera.
Como a aceleração do bloco é a mesma que a da fita podemos escrever:
Queremos no final das contas a aceleração do centro de massa da esfera .
Passo 2
(a) Escreva a equação do movimento para o bloco acompanhada do respectivo diagrama de corpo livre.
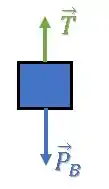
O bloco está sujeito apenas à duas forças, a força peso e a força de tração :
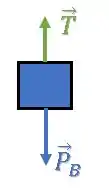
Agora, só falta escrever a segunda lei de Newton para o bloco.
Como o bloco desce, a força peso do bloco vence a “briga” e tem o mesmo sinal da aceleração do bloco:
Passo 3
(b) Escreva a equação do movimento de translação da esfera acompanhada do respectivo diagrama de corpo livre. Faça o mesmo para a equação do movimento de rotação da esfera. Escreva também a condição de rolamento sem deslizamento.
Opaa, vários pedidos... vamos um por um.
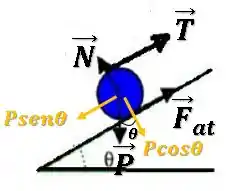
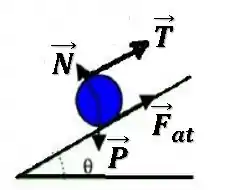
Vamos começar com o diagrama de forças da esfera.
A força peso está para baixo, a força normal está perpendicular ao plano, a força de tração está na direção da fita (como a polia é ideal, tem o mesmo valor que a tração no bloco).
A força de atrito não conseguimos saber ao certo seu sentido, pois dependendo dos valores de massas e dimensões, ela poderia estar em qualquer um dos sentidos.
Então, vamos “chutar” para cima da rampa e podemos ver que lá na frente isso vai cortar e não influenciar no que queremos.
Caso tivéssemos valores numérico, bastava substituí-los e caso achássemos um valor negativo de , significa que a força estará no sentido contrário que chutamos inicialmente.
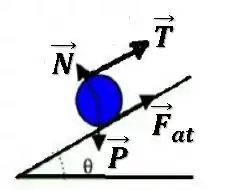
Para a equação de translação da esfera, vamos aplicar novamente a segunda lei de Newton.
Os eixos já estão definidos na imagem do enunciado, eixo para cima da rampa e eixo , perpendicular à rampa.
Vamos decompor a força peso nesses eixos:
Para o eixo :
Para o eixo , temos um equilíbrio de forças:
Passo 4
Vamos agora escrever a equação de rotação da esfera.
O torque resultante será a soma dos torques de todas as forças com relação ao centro de massa da esfera:
A força peso está aplicada no centro de massa da esfera, portanto ela não gera torque:
A força normal é calculada pelo seguinte produto vetorial:
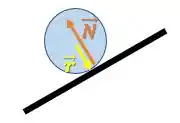
Como esses vetores estão na mesma direção, o produto vetorial resultará em zero:
Já os torques das forças de atrito e de tração serão:
Ambas são perpendiculares aos seus vetores , além disso, eles estão na periferia da esfera , então, o módulo de seus torques serão:
Entretanto, tenta fazer a esfera girar no sentido horário enquanto tenta fazer a esfera girar no sentido anti-horário, portanto, esses torques tem sinais contrários.
Como a esfera está subindo, vamos considerar o sentido de sua aceleração (horário) positivo:
Além disso, queremos a condição de rolamento sem deslizamento:
Como a aceleração do bloco também se relaciona com isso, podemos escrever também aquela condição já dada no enunciado:
Passo 5
(c) Resolva o sistema de equações e encontre uma expressão literal para o módulo da aceleração do CM da esfera em função dos dados fornecidos.
Temos que tomar cuidado para não nos enrolarmos.
Temos as seguintes equações:

Eu sei, são muitas equações, mas vamos passo a passo...
Queremos achar encontrar a aceleração do centro de massa da esfera .
Então um bom primeiro passo é retirar aceleração angular substituindo por . Logo, vamos usar a relação (5) em (4):
Além disso, vamos usar a expressão para o momento de inércia de uma esfera com um eixo passando pelo seu centro:
Então, ficamos com:
Podemos cortar aquele com um do lado esquerdo e o outro no denominador:
Vamos chamar essa equação de (7):
Guarda essa (7) aí.
Agora vamos pegar essa expressão (1):
E usar a relação (6):
Então, temos:
Vamos chamar essa equação de (8):
Passo 6
Agora, o próximo passo é pegar tudo que tem , tirando as equações iniciais que já usamos:
Beleza, tudo que tem está do lado direito, então vamos somar essas equações para eliminar e , que não são dados.
Somando (2) com (7):
Agora, para eliminar , vamos somar isso com :
E FINALMENTE...

Resposta
(a)
(b)
Translação:
Rotação:
Relações para que não haja deslizamento:
(c)