A posição de uma partícula em metros é descrita pelo vetor posição

Seja o ângulo em radianos que o vetor velocidade da partícula faz com o eixo no instante . Pode-se afirmar que é igual a:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Vamos lá!! Ele dá o vetor posição da partícula e pede informação do vetor velocidade.

Como que a gente acha esse cara?

Acompanha comigo:

Então, substituindo:

Derivando isso daí:

Maravilha! Já temos o vetor velocidade em função do tempo. Mas ele quer informação de quando o instante é . Então, vamos ver como é a cara do vetor velocidade em .

Resolvendo isso:

É essa cara aqui que ele tem:

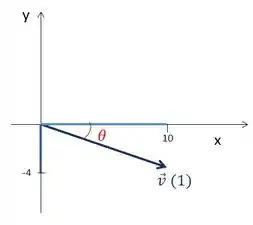
Já marquei o ângulo que o vetor faz com a horizontal.

Se a gente calcular a tangente desse ângulo, temos:

Simplificando:

Isso quer dizer que o ângulo é:

Que é a nossa opção F.

Show de bola?