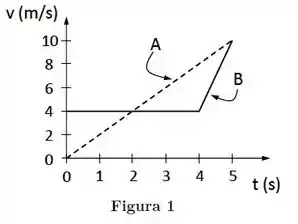
Dois carros (A e B) partem da mesma posição inicial em e movem-se em
pistas retas paralelas. Seus gráficos da velocidade em função do tempo são mostrados na Figura 1.
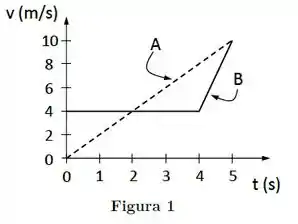
Considere as afirmativas abaixo:
(I) A variação da velocidade de B é maior que a de A no intervalo entre e .
(II) As acelerações de A e B são iguais no instante .
(III) A aceleração média no intervalo entre e é maior para A.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(a) I
(b) II
(c) III
(d) I e II
(e) I e III
(f) II e III
(g) Todas
(h) Nenhuma
Passo 1
Vamos lá! Olhando pra esse gráfico, de velocidade versus tempo, a gente já pode identificar algumas coisas:
1) O movimento de A é caracterizado por uma linha reta no gráfico x isso quer dizer que se trata de um MUV, logo, a acelelaração é constante. E é numericamente igual ao coeficiente angular dessa reta, ou seja, a tangente ;)... beleza até aqui?
2) o movimento de B começa com uma reta horizontal e depois se transforma em uma reta inclinada, como falamos antes, a inclinação tá relacionada a aceleração, então se a inclinação mudou, a aceleração também mudou. E aí? Isso é muito ruim? Não!! É só tomar cuidado na hora de analisar, pois só podemos usar aquelas equações do MUV para movimentos com a aceleração constante, então vamos ter que dividir a análise do B nessas duas partes de inclinações diferentes. Ok?!
Vamos ler com calma cada alternativa
Passo 2
(I) A variação da velocidade de B é maior que a de A no intervalo entre e .
Primeiro, vamos olhar para a variação da velocidade do A...A velocidade de A quando é e quando , temos , então:
Agora, vamos ver a variação da velocidade do B...A velocidade de B quando é e quando , temos , então:
Logo:
Então essa alternativa tá errada!
Passo 3
(II) As acelerações de A e B são iguais no instante .
Vamos lembrar da equação do MUV:
Para o movimento A, a aceleração é a mesma desde até , a velocidade em é e a velocidade inicial é nula. Então:
Agora, vamos ver para o B. Como falamos antes, desde até a aceleração do B é zero (reta horizontal ou seja, velocidade constante), então pra achar a aceleração do B em vamos considerar a velocidade inicial como sendo e o tempo inicial em (que é a parte do gráfico com inclinação)
Então, como queremos, a aceleração em , só precisamos esperar .
Logo, as acelerações são diferentes, e essa alternativa está errada!
Passo 4
(III) A aceleração média no intervalo entre e é maior para A.
Acelaração média nada mais é do que:
Entre e é:
Para o movimento A, temos:
Para o movimento B, temos:
Logo,
Então essa alternativa tá correta!!
Resposta
Alternativa C.