Dois carros (A e B) partem da mesma posição inicial em e movem-se em pistas retas paralelas. Seus gráficos da velocidade em função do tempo são mostrados na Figura 1.

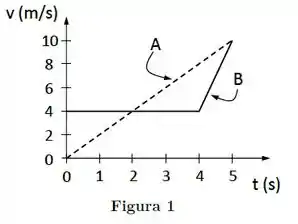
A distância entre os carros no instante é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Vamos achar a posição do A. Lembrando que temos um MUV, então vamos usar essa equação da posição em função do tempo:

A gente não sabe qual é a posição inicial do A e do B, mas a gente sabe que elas são iguais, então vamos chamar de mesmo, ok?

A velocidade inicial do A é . E a aceleração é dada pela tangente do gráfico, ou seja:

Então a função posição de A é:

A posição do A em , vai ser:

Show de bola! Agora vamos ver qual é a posição do B.

Aqui temos que ter um pouco mais de atenção. Pois a inclinação da reta do gráfico de B muda, ou seja, a aceleração do B muda ao longo desses 5 segundos.

Na primeira parte temos aceleração nula, pois a velocidade é constante. Então a posição em função do tempo é dada pela equação do movimento uniforme:

Entre e , temos:

Então, quando é o fim do movimento uniforme e início do MUV. Ou seja, essa posição que acabamos de achar vai ser a posição inicial do MUV, e a aceleração é dada pela tangente e vale .

Então a posição do B em é:

Maravilha!! Já sabemos as posições dos dois corpos em , pra achar a distância entre eles é só subtrair um pelo outro:

Uhuul!! Isso é a letra G.