Uma partícula de massa executa um MCU no sentido anti-horário com raio e período . O centro da sua trajetória coincide com a origem do sistema de coordenadas.
No instante , o vetor posição da partícula em metros é . No instante , a força centrípeta (em newtons) agindo na partícula é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Opa! Vamos ver o que a gente tem nesse caso:
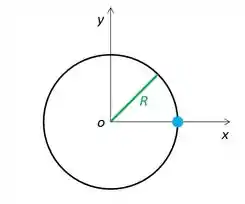
O raio R vale . Já coloquei a nossa partícula ali na posição inicial, que o exercício dá pra gente, .
Bom, isso é um movimento circular uniforme, isso quer dizer que distâncias iguais são percorridas em intervalos de tempo iguais.
Aí olha só... Vamos dividir essa circunferência em 4:
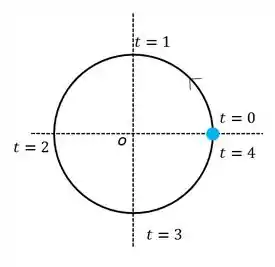
A partícula percorre cada da circunferência em , pois o período, que é o tempo necessário para ela voltar a posição inicial é . Show?
Então, no instante , vamos ter:
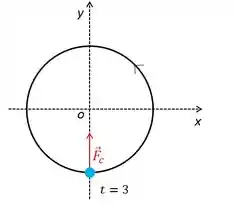
Com isso a gente já sabe a direção e o sentido da força centrípeta, que aponta sempre para o centro da trajetória curvilínea. Logo, já sabemos que é alguma coisa assim:
Agora, vamos descobrir quanto vale o móduo da força centrípeta.
Passo 2
O módulo da força centrípeta é dado por:
A massa da partícula e o raio da trajetória nós temos. Só falta a velocidade.
Como que a gente acha isso?
Bom, a velocidade nada mais é do que o quanto a partícula andou em um intervalo de tempo, certo? Então, o período é o tempo necessário para ela completar 1 volta completa, certo? E uma volta equivale a andar um comprimento igual à . Então:
Para 1 volta:
Substituindo os valores:
Essa é a velocidade da partícula, então substituindo na equação da força centrípeta, temos:
Substituindo os valores:
Logo, a força centrípeta no instante é:
Essa é a letra B!!
Show of ball?
Resposta
Alternativa B.