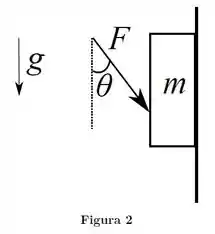
A Figura 2 mostra um bloco de massa , inicialmente em repouso, em contato com uma parede vertical. Os coecientes de atrito estático e cinético entre o bloco e a parede são, respectivamente, e .
Uma força de módulo encontra-se aplicada ao bloco, fazendo um ângulo com a vertical. O ângulo é tal que
e . Considere a aceleração gravitacional de módulo .
(a) Faça o diagrama de corpo livre do bloco, desenhando todas as forças que atuam sobre ele.
(b) Calcule o módulo da força normal que a parede exerce sobre o bloco.
(c) O bloco se move? Justique sua resposta.
(d) Calcule os módulos da força de atrito e da aceleração do bloco.
Passo 1
(a)
Show! Vamos lá... ele pede o diagrama de corpo livre do bloco. Então, a gente tem o peso (poia o bloco sofre atração gravitacional), a normal (pois o bloco está em contato com uma superfície), a força de atrito (já que a superfície não é lisa) e a força , ok?
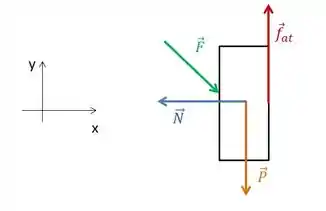
Maravilha!! Vamos pra próxima!
Passo 2
(b)
Notem que no eixo x não há movimento. O bloco pode escorregar, ou não, mas esse movimento é só na vertical.
Como o bloco começa no repouso e não há movimento na horizontal temos que:
Temos que decompor a força , já que ela te componentes na vertical e na horizontal:
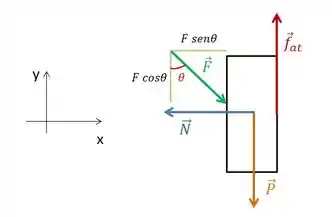
Então, na horizontal, temos:
Substituindo os valores, temos:
Show!!
Passo 3
(c)
As forças que atuam na direção y são: o peso, uma componente da força e a força de atrito. Então, usando o sistema de orientação da figura, a força resultante em y é:
E para não ter movimento, temos que a força resultante deve ser zero. Ou seja:
Vamos substituir os valores do peso, da F e do :
Resolvendo isso, temos que:
Então o que encontramos foi que: Para o bloco permanecer em equilíbrio a força de arito deve ser igual a .
Agora, vamos checar se isso de fato ocorre. Como? Bem, vamos ver quanto vale a forçade atrito estática máxima. Ela tem essa cara:.
Se o valor da força de atrito máxima for maior que 28 N, então o bloco permanece em repouso. Mas se o valor for menor que 28 N, então a não é suficiente para manter tudo parado, e o bloco vai se mover.
Vamos lá
Huuum... Então a nossa é menor que 28 N. Logo, o bloquinho vai escorregar.
Passo 4
(d)
Agora ele pediu pra gente calcular a força de atrito e a aceleração do bloco.
Você pode ficar tentado a pensar “já sei quanto vale a força de atrito...acabei de calcular na letra c”.
Calma lá!!!
O que calculamos foi a força de atrito ESTÁTICA. Ou seja, a força ecessária para manter tudo parado. Mas vimos que ocorre movimento, então a força de atrito que fato ocorre é a força de atrito CINÉTICA.
Substituindo os valores:
Beleza, se temos o valor da , podemos usar a segunda lei de newton na vetical:
Substituindo os valores:
Resolvendo isso:
Essa é a aceleração do bloco. Na direção x a aceleração é nula, pois não há movimento.
Show???
Resposta
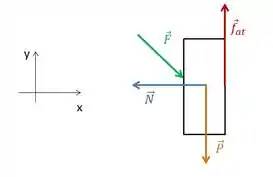 A)
A)
B)
C) O bloco se move. A força de atrito é menor do que a força de atrito estática máxima.
D)