P2 de Física 1 da UFRJ - 2014.1

Uma esfera oca e rígida de massa e raio tem momento de inércia relativo a um eixo que passa pelo seu centro de massa. Relativamente a um eixo que tangencia a periferia da esfera e é paralelo ao eixo que passa pelo centro de massa, o momento de inércia da esfera é

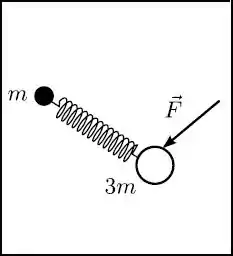
Dois discos de massas e estão ligados por uma mola ideal comprimida sobre uma mesa horizontal lisa. Em um dado instante a força da mola sobre o primeiro disco é e uma força paralela ao plano da mesa está aplicada sobre o segundo disco, como mostra a figura (mesa vista de cima). No instante considerado a aceleração do centro de massa do sistema constituído pelos discos e pela mola é

1. ;
2. ;
3. ;
4. ;
5. ;

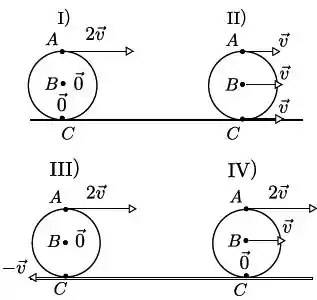
Um cilindro solido rola sem deslizar, com velocidade angular constante, sobre uma superfície horizontal. Dentre os diagramas abaixo, , , e , aquele que representa corretamente os vetores velocidade (indicados por setas) dos pontos (topo), (base) e (centro), pontos pertencentes a periferia do cilindro (seção reta), em relação a um referencial fixo na Terra é

5. Nenhum deles

Um carro tem uma roda de massa e raio com momento de inércia relativo ao seu eixo de rotação que passa pelo seu centro de massa. O carro arranca em movimento retilíneo com a roda patinando na pista de modo que a velocidade de seu centro de massa esteja relacionada com sua velocidade angular de rotação por meio de . Nesse caso, a energia cinética da roda é

1. ;
2. ;
3. ;
4. ;
5. ;

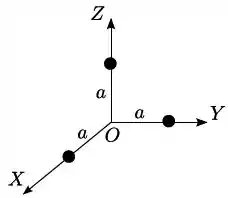
Um sistema é constituído de três partículas de mesma massa localizadas nos semi-eixos positivos , e a uma mesma distância da origem, como indica a figura. O vetor posição do centro de massa do sistema é

1. ;
2. ;
3. ;
4. ;
5. ;

Um disco fino e homogêneo de raio encontra-se em repouso sobre uma superfície horizontal sem atrito. Num dado instante aplicam-se na periferia do disco três forças tangenciais e uma radial, todas de mesma intensidade com direções, sentidos e pontos de aplicação conforme indicados na figura. Nesse instante, o módulo do torque resultante em relação ao centro do disco é

1. ;
2. ;
3. ;
4. ;
5. ;

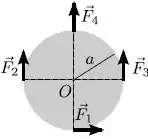
Um menino encontra-se parado em uma das extremidades de um barco que está em um lago tranquilo. Inicialmente o conjunto (barco-menino) move-se com velocidade constante, em relação a um referencial inercial fixo colocado na margem do lago. Num dado instante o menino move-se para a outra extremidade do barco e ao chegar neste lugar ele para. Para o sistema barco-menino, desprezando-se o atrito entre o barco e a água, pode-se afirmar que

1. A sua velocidade antes do menino se movimentar é diferente de depois do menino parar.
2. A sua velocidade é a mesma de antes do início do movimento do menino e depois do menino parar.
3. A sua velocidade pode ser nula depois do menino parar.
4. Não se pode determinar a sua velocidade, pois não se conhece a velocidade do menino sobre o barco.
5. Não se pode determinar a sua velocidade, a menos que sejam conhecidas as massas do menino e do barco.

Um corpo rígido gira em torno de um eixo fixo com velocidade angular constante quando, a partir do instante , passa a ter uma aceleração angular constante de módulo e sentido oposto ao da velocidade angular. Denotando por o tempo gasto pelo corpo para sua velocidade angular atingir o valor nulo e por o seu deslocamento angular do instante até o instante , podemos afirmar que

1. e ;
2. e ;
3. e ;
4. e ;
5. e ;

Duas partículas inicialmente separadas sofrem uma colisão totalmente inelástica na ausência de forças externas. Pode-se afirmar, sobre o sistema constituído pelas duas partículas, que

1. A energia cinética do centro de massa do sistema é a mesma antes e depois da colisão;
2. O módulo da velocidade do centro de massa do sistema é menor antes do que depois da colisão;
3. A energia cinética total do sistema é a mesma antes e depois da colisão;
4. O módulo da velocidade do centro de massa do sistema é maior antes do que depois da colisão;
5. A energia cinética total do sistema é menor antes do que depois da colisão.

Duas partículas de mesma massa caem verticalmente e colidem com uma mesa horizontal lisa com a mesma velocidade. Uma das partículas colide elasticamente com a mesa sem sair da vertical e a outra colide de forma totalmente inelástica com a mesa. Denotando por a variação do momento linear da primeira particular na colisão elástica, por a variação do momento linear da segunda partícula em sua colisão totalmente inelástica, podemos afirmar que

3. e

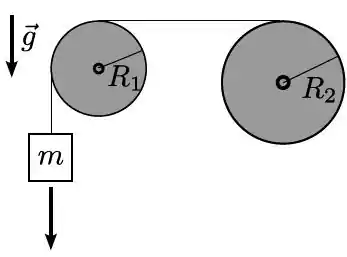
Um fio inextensível de massa desprezível é enrolado diversas vezes em torno da periferia de um cilindro maciço de raio , segue horizontalmente até a periferia de outro cilindro de raio , pela qual passa e segue verticalmente, até sua extremidade, na qual está suspenso um bloco de massa . Os cilindros, cada um também de massa , são homogêneos e podem girar sem atrito, cada um em torno de seu eixo fixo. O bloco desce verticalmente puxando o fio que fica tenso e faz os cilindros girarem, sem deslizar sobre suas periferias. (O momento de inércia de um cilindro homogêneo de massa e raio relativo ao seu eixo é )

1. Faça um diagrama das forças externas que agem sobre o cilindro de raio
2. Calcule o módulo da aceleração com que desce o bloco.
3. Obtenha o módulo da aceleração angular de cada cilindro.
4. Calcule o módulo da tensão no trecho vertical do fio e o módulo da tensão no trecho horizontal do fio.

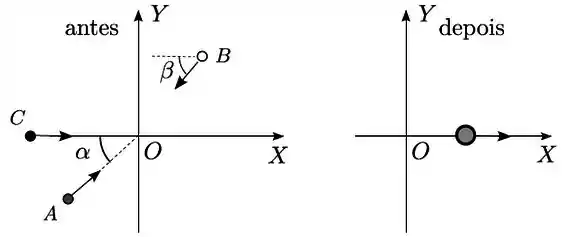
Três partículas , e , deslizando sobre uma mesa horizontal sem atrito, se aproximam da origem de um sistema de eixos no plano da mesa. Todas as três partículas atingem a origem simultaneamente e permanecem unidas após a colisão, sem perder contato com a mesa, deslocando-se ao longo do eixo no sentido positivo com velocidade de módulo desconhecida. As partículas , e têm massas respectivas , e , onde é uma constante conhecida. Antes da colisão as partículas têm velocidades de módulos respectivos , e , onde é uma constante conhecida. A partícula tem velocidade na direção e sentido do eixo e a partícula tem velocidade com direção e sentido indicados na figura por meio do ângulo conhecido . A velocidade da partícula tem o sentido indicado na figura mas sua direção é desconhecida e indicada pelo ângulo a ser determinado. Calcule

1. O ângulo ;
2. O módulo da velocidade após a colisão em função de ;
3. A variação da energia cinética do sistema formado pelas três partículas no processo de colisão.