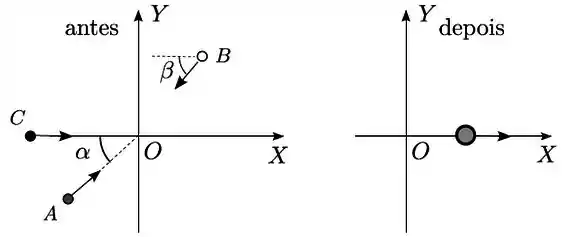
Três partículas , e , deslizando sobre uma mesa horizontal sem atrito, se aproximam da origem de um sistema de eixos no plano da mesa. Todas as três partículas atingem a origem simultaneamente e permanecem unidas após a colisão, sem perder contato com a mesa, deslocando-se ao longo do eixo no sentido positivo com velocidade de módulo desconhecida. As partículas , e têm massas respectivas , e , onde é uma constante conhecida. Antes da colisão as partículas têm velocidades de módulos respectivos , e , onde é uma constante conhecida. A partícula tem velocidade na direção e sentido do eixo e a partícula tem velocidade com direção e sentido indicados na figura por meio do ângulo conhecido . A velocidade da partícula tem o sentido indicado na figura mas sua direção é desconhecida e indicada pelo ângulo a ser determinado. Calcule
- O ângulo ;
- O módulo da velocidade após a colisão em função de ;
- A variação da energia cinética do sistema formado pelas três partículas no processo de colisão.
Passo 1
Como não temos ação de forças externas o momento linear se conserva, precisamos então achar as velocidades antes da colisão para calcularmos os momentos lineares, isso porque
Vamos começar pela partícula ,
Agora vamos para a velocidade da partícula , usando a regra do “COlado/SEparado”
Resultando em
Passo 2
Agora para a partícula
Resultando em
Passo 3
Falta agora a velocidade do conjunto após a colisão
Passo 4
Os momentos lineares vão ser
Passo 5
Como o momento linear do sistema após a colisão só tem componente horizontal devemos ter
Como e são menores que
Passo 6
b)
Igualando as componentes horizontais dos momentos lineares antes e depois da colisão
Passo 7
c)
A energia cinética inicial vai ser
Lembrando que na energia cinética usamos o módulo da velocidade
Passo 8
A energia cinética final vai ser
Passo 9
A variação de energia cinética vai ser