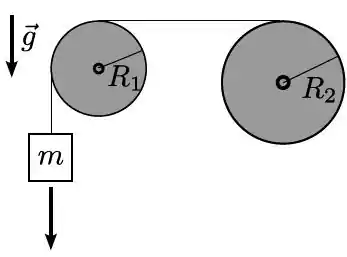
Um fio inextensível de massa desprezível é enrolado diversas vezes em torno da periferia de um cilindro maciço de raio , segue horizontalmente até a periferia de outro cilindro de raio , pela qual passa e segue verticalmente, até sua extremidade, na qual está suspenso um bloco de massa . Os cilindros, cada um também de massa , são homogêneos e podem girar sem atrito, cada um em torno de seu eixo fixo. O bloco desce verticalmente puxando o fio que fica tenso e faz os cilindros girarem, sem deslizar sobre suas periferias. (O momento de inércia de um cilindro homogêneo de massa e raio relativo ao seu eixo é )
- Faça um diagrama das forças externas que agem sobre o cilindro de raio
- Calcule o módulo da aceleração com que desce o bloco.
- Obtenha o módulo da aceleração angular de cada cilindro.
- Calcule o módulo da tensão no trecho vertical do fio e o módulo da tensão no trecho horizontal do fio.
Passo 1
a)
O DCL do cilindro de raio fica
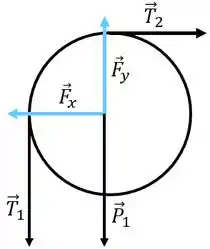
As forças em azul são a reação horizontal e vertical do pino que prende o cilindro.
Passo 2
b)
Vamos agora fazer o DCL do bloco
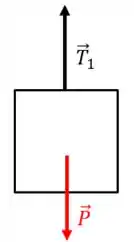
Considerando que o bloco está caindo, e sendo o módulo da sua aceleração
Passo 3
Vamos agora fazer o equilíbrio da rotação no disco de raio , como o disco roda no sentido anti-horário
Isso porque a tração faz girar no sentido anti-horário e a tração faz girar no sentido horário.
O momento de inércia do cilindro é
Além disso
Juntando tudo
Passo 4
Agora no cilindro de raio a única força que faz torque é a tração
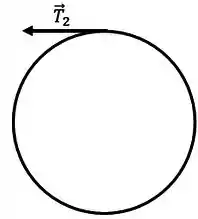
Dessa força, como ele gira no sentido anti-horário
O momento de inércia do cilindro é
Além disso
Juntando tudo
Passo 5
Vamos ter o seguinte sistema
Somando essas equações
Passo 6
c)
Já vimos nos outros passos que
E
Então
E
Passo 7
d)
As trações vão ser
Passo 8
E
Resposta
a) 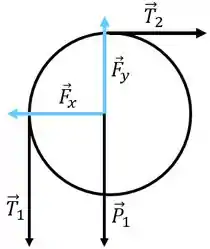
b)
c)
d)